problem_id
stringlengths 12
21
| task_type
stringclasses 1
value | prompt
stringlengths 0
13.6k
| verification_info
stringlengths 20
1.24k
| metadata
stringclasses 89
values | __index_level_0__
int64 0
776k
|
|---|---|---|---|---|---|
numina_1.5_0
|
verifiable_math
|
Problem 4. A $5 \times 100$ table is divided into 500 unit square cells, where $n$ of them are coloured black and the rest are coloured white. Two unit square cells are called adjacent if they share a common side. Each of the unit square cells has at most two adjacent black unit square cells. Find the largest possible value of $n$.
|
{"ground_truth": "302"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 0
|
numina_1.5_1
|
verifiable_math
|
Problem 3. Find all the triples of integers $(a, b, c)$ such that the number
$$
N=\frac{(a-b)(b-c)(c-a)}{2}+2
$$
is a power of 2016 .
(A power of 2016 is an integer of the form $2016^{n}$, where $n$ is a non-negative integer.)
|
{"ground_truth": "(,b,)=(k+2,k+1,k),k\\in\\mathbb{Z}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 1
|
numina_1.5_2
|
verifiable_math
|
Problem 2. Let $n$ three-digit numbers satisfy the following properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
{"ground_truth": "5"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 2
|
numina_1.5_3
|
verifiable_math
|
## Problem 2
Let the circles $k_{1}$ and $k_{2}$ intersect at two distinct points $A$ and $B$, and let $t$ be a common tangent of $k_{1}$ and $k_{2}$, that touches $k_{1}$ and $k_{2}$ at $M$ and $N$, respectively. If $t \perp A M$ and $M N=2 A M$, evaluate $\angle N M B$.
|
{"ground_truth": "45"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 3
|
numina_1.5_4
|
verifiable_math
|
## Problem 4
Find all positive integers $x, y, z$ and $t$ such that
$$
2^{x} \cdot 3^{y}+5^{z}=7^{t}
$$
|
{"ground_truth": "3,1,=2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 4
|
numina_1.5_5
|
verifiable_math
|
Problem 2. For any set $A=\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ of five distinct positive integers denote by $S_{A}$ the sum of its elements, and denote by $T_{A}$ the number of triples $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ for which $x_{i}+x_{j}+x_{k}$ divides $S_{A}$.
Find the largest possible value of $T_{A}$.
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 5
|
numina_1.5_6
|
verifiable_math
|
Problem 4. Let $M$ be a subset of the set of 2021 integers $\{1,2,3, \ldots, 2021\}$ such that for any three elements (not necessarily distinct) $a, b, c$ of $M$ we have $|a+b-c|>10$. Determine the largest possible number of elements of $M$.
|
{"ground_truth": "1006"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 6
|
numina_1.5_7
|
verifiable_math
|
Problem 1. Find all distinct prime numbers $p, q$ and $r$ such that
$$
3 p^{4}-5 q^{4}-4 r^{2}=26
$$
|
{"ground_truth": "p=5,q=3,r=19"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 7
|
numina_1.5_8
|
verifiable_math
|
Problem 2. Consider an acute triangle $A B C$ with area S. Let $C D \perp A B \quad(D \in A B)$, $D M \perp A C \quad(M \in A C)$ and $\quad D N \perp B C \quad(N \in B C)$. Denote by $H_{1}$ and $H_{2}$ the orthocentres of the triangles $M N C$ and $M N D$ respectively. Find the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$ in terms of $S$.
|
{"ground_truth": "S"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 8
|
numina_1.5_9
|
verifiable_math
|
Problem 4. For a positive integer $n$, two players A and B play the following game: Given a pile of $s$ stones, the players take turn alternatively with A going first. On each turn the player is allowed to take either one stone, or a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming both $\mathrm{A}$ and $\mathrm{B}$ play perfectly, for how many values of $s$ the player A cannot win?
|
{"ground_truth": "n-1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 9
|
numina_1.5_10
|
verifiable_math
|
Problem 1. Find all pairs $(a, b)$ of positive integers such that
$$
11 a b \leq a^{3}-b^{3} \leq 12 a b
$$
|
{"ground_truth": "(5,2)"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 10
|
numina_1.5_11
|
verifiable_math
|
Problem 4. We call an even positive integer $n$ nice if the set $\{1,2, \ldots, n\}$ can be partitioned into $\frac{n}{2}$ two-element subsets, such that the sum of the elements in each subset is a power of 3 . For example, 6 is nice, because the set $\{1,2,3,4,5,6\}$ can be partitioned into subsets $\{1,2\},\{3,6\},\{4,5\}$. Find the number of nice positive integers which are smaller than $3^{2022}$.
|
{"ground_truth": "2^{2022}-1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 11
|
numina_1.5_12
|
verifiable_math
|
## Problem 1.
Find all pairs $(a, b)$ of positive integers such that $a!+b$ and $b!+a$ are both powers of 5 .
|
{"ground_truth": "(1,4),(4,1),(5,5)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 12
|
numina_1.5_13
|
verifiable_math
|
Problem 1. Find all triples $(a, b, c)$ of real numbers such that the following system holds:
$$
\left\{\begin{array}{l}
a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \\
a^{2}+b^{2}+c^{2}=\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}
\end{array}\right.
$$
|
{"ground_truth": "(,b,)=(,\\frac{1}{},1),(,\\frac{1}{},-1)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 13
|
numina_1.5_14
|
verifiable_math
|
Problem 4. Find all pairs $(p, q)$ of prime numbers such that
$$
1+\frac{p^{q}-q^{p}}{p+q}
$$
is a prime number.
|
{"ground_truth": "(2,5)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 14
|
numina_1.5_15
|
verifiable_math
|
Problem 4. Consider a regular $2 n$-gon $P, A_{1} A_{2} \ldots A_{2 n}$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We color the sides of $P$ in 3 different colors (ignore the vertices of $P$, we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to $P$, points of at most 2 different colors on $P$ can be seen. Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one of the sides is colored differently).
|
{"ground_truth": "6n"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 15
|
numina_1.5_16
|
verifiable_math
|
Problem 1. Find all prime numbers $a, b, c$ and positive integers $k$ which satisfy the equation
$$
a^{2}+b^{2}+16 \cdot c^{2}=9 \cdot k^{2}+1
$$
|
{"ground_truth": "(37,3,3,13),(17,3,3,7),(3,37,3,13),(3,17,3,7),(3,3,2,3)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 16
|
numina_1.5_17
|
verifiable_math
|
Problem 2. Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of the expression
$$
A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}
$$

$19^{\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia
|
{"ground_truth": "3"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 17
|
numina_1.5_18
|
verifiable_math
|
A2. Let $a$ and $b$ be positive real numbers such that $3 a^{2}+2 b^{2}=3 a+2 b$. Find the minimum value of
$$
A=\sqrt{\frac{a}{b(3 a+2)}}+\sqrt{\frac{b}{a(2 b+3)}}
$$
|
{"ground_truth": "\\frac{2}{\\sqrt{5}}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 18
|
numina_1.5_19
|
verifiable_math
|
C1. Consider a regular $2 n+1$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the largest positive integer for which such a coloring is possible.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 19
|
numina_1.5_20
|
verifiable_math
|
C2. Consider a regular $2 n$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one side is colored differently).
|
{"ground_truth": "6n"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 20
|
numina_1.5_21
|
verifiable_math
|
NT3. Find all pairs of positive integers $(x, y)$ such that $2^{x}+3^{y}$ is a perfect square.
|
{"ground_truth": "(4,2)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 21
|
numina_1.5_22
|
verifiable_math
|
NT4. Solve in nonnegative integers the equation $5^{t}+3^{x} 4^{y}=z^{2}$.
|
{"ground_truth": "(,x,y,z)=(1,0,1,3),(0,1,0,2),(2,2,2,13),(0,1,2,7)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 22
|
numina_1.5_23
|
verifiable_math
|
NT5. Find all positive integers $n$ such that there exists a prime number $p$, such that
$$
p^{n}-(p-1)^{n}
$$
is a power of 3 .
Note. A power of 3 is a number of the form $3^{a}$ where $a$ is a positive integer.
|
{"ground_truth": "2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 23
|
numina_1.5_24
|
verifiable_math
|
A4. Solve the following equation for $x, y, z \in \mathbb{N}$
$$
\left(1+\frac{x}{y+z}\right)^{2}+\left(1+\frac{y}{z+x}\right)^{2}+\left(1+\frac{z}{x+y}\right)^{2}=\frac{27}{4}
$$
|
{"ground_truth": "z"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 24
|
numina_1.5_25
|
verifiable_math
|
A5. Find the largest positive integer $n$ for which the inequality
$$
\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c} \leq \frac{5}{2}
$$
holds for all $a, b, c \in[0,1]$. Here $\sqrt[1]{a b c}=a b c$.
|
{"ground_truth": "3"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 25
|
numina_1.5_26
|
verifiable_math
|
G4. Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$, and let $O, H$ be the triangle's circumcenter and orthocenter respectively. Let also $A^{\prime}$ be the point where the angle bisector of angle $B A C$ meets $\Gamma$. If $A^{\prime} H=A H$, find the measure of angle $B A C$.
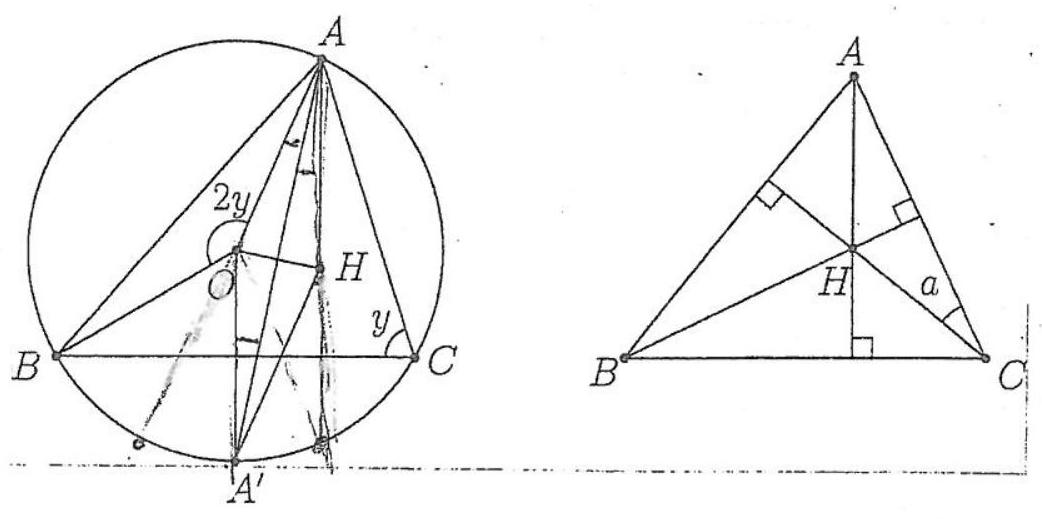
Figure 4: Exercise G4.
|
{"ground_truth": "60"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 26
|
numina_1.5_27
|
verifiable_math
|
NT5. Find all the positive integers $x, y, z, t$ such that $2^{x} \cdot 3^{y}+5^{z}=7^{t}$.
|
{"ground_truth": "3,1,=2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 27
|
numina_1.5_28
|
verifiable_math
|
A1. Find all ordered triples $(x, y, z)$ of real numbers satisfying the following system of equations:
$$
\begin{aligned}
x^{3} & =\frac{z}{y}-2 \frac{y}{z} \\
y^{3} & =\frac{x}{z}-2 \frac{z}{x} \\
z^{3} & =\frac{y}{x}-2 \frac{x}{y}
\end{aligned}
$$
|
{"ground_truth": "(1,1,-1),(1,-1,1),(-1,1,1),(-1,-1,-1)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 28
|
numina_1.5_29
|
verifiable_math
|
A2. Find the largest possible value of the expression $\left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|$ where $x$ is a real number.
|
{"ground_truth": "\\sqrt{5}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 29
|
numina_1.5_30
|
verifiable_math
|
N3. Find all ordered pairs $(a, b)$ of positive integers for which the numbers $\frac{a^{3} b-1}{a+1}$ and $\frac{b^{3} a+1}{b-1}$ are positive integers.
|
{"ground_truth": "(1,3),(2,2),(3,3)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 30
|
numina_1.5_31
|
verifiable_math
|
N5. Find all ordered triples $(x, y, z)$ of positive integers satisfying the equation
$$
\frac{1}{x^{2}}+\frac{y}{x z}+\frac{1}{z^{2}}=\frac{1}{2013}
$$
|
{"ground_truth": "(x,y,z)=(2013n,2013n^{2}-2,2013n)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 31
|
numina_1.5_32
|
verifiable_math
|
N6. Find all ordered triples $(x, y, z)$ of integers satisfying the following system of equations:
$$
\begin{aligned}
x^{2}-y^{2} & =z \\
3 x y+(x-y) z & =z^{2}
\end{aligned}
$$
|
{"ground_truth": "(0,0,0),(1,0,1),(0,1,-1),(1,2,-3),(2,1,3)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 32
|
numina_1.5_33
|
verifiable_math
|
## A1 MLD
Let $x, y, z$ be real numbers, satisfying the relations
$$
\left\{\begin{array}{l}
x \geq 20 \\
y \geq 40 \\
z \geq 1675 \\
x+y+z=2015
\end{array}\right.
$$
Find the greatest value of the product $P=x \cdot y \cdot z$.
|
{"ground_truth": "48407500"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 33
|
numina_1.5_34
|
verifiable_math
|
## A2 ALB
3) If $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0$, find the value of $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015$.
|
{"ground_truth": "1898"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 34
|
numina_1.5_35
|
verifiable_math
|
NT1 SAU
What is the greatest number of integers that can be selected from a set of 2015 consecutive numbers so that no sum of any two selected numbers is divisible by their difference?
|
{"ground_truth": "672"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 35
|
numina_1.5_36
|
verifiable_math
|
## C1 BUL
A board $n \times n(n \geq 3)$ is divided into $n^{2}$ unit squares. Integers from 0 to $n$ included are written down: one integer in each unit square, in such a way that the sums of integers in each $2 \times 2$ square of the board are different. Find all $n$ for which such boards exist.
|
{"ground_truth": "3\\leqn\\leq6"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 36
|
numina_1.5_37
|
verifiable_math
|
## C3 ALB
Positive integers are put into the following table
| 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | | |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| 2 | 5 | 9 | 14 | 20 | 27 | 35 | 44 | | |
| 4 | 8 | 13 | 19 | 26 | 34 | 43 | 53 | | |
| 7 | 12 | 18 | 25 | 33 | 42 | | | | |
| 11 | 17 | 24 | 32 | 41 | | | | | |
| 16 | 23 | | | | | | | | |
| $\ldots$ | | | | | | | | | |
| $\ldots$ | | | | | | | | | |
Find the number of the line and column where the number 2015 stays.
|
{"ground_truth": "2015"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 37
|
numina_1.5_38
|
verifiable_math
|
C4
GRE
Let $n \geq 1$ be a positive integer. A square of side length $n$ is divided by lines parallel to each side into $n^{2}$ squares of side length 1 . Find the number of parallelograms which have vertices among the vertices of the $n^{2}$ squares of side length 1 , with both sides smaller or equal to 2 , and which have the area equal to 2 .
|
{"ground_truth": "7n^{2}-12n+1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 38
|
numina_1.5_39
|
verifiable_math
|
C3 The nonnegative integer $n$ and $(2 n+1) \times(2 n+1)$ chessboard with squares colored alternatively black and white are given. For every natural number $m$ with $1<m<2 n+1$, an $m \times m$ square of the given chessboard that has more than half of its area colored in black, is called a $B$-square. If the given chessboard is a $B$-square, find in terms of $n$ the total number of $B$-squares of this chessboard.
|
{"ground_truth": "\\frac{(n+1)(2n^{2}+4n+3)}{3}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 39
|
numina_1.5_40
|
verifiable_math
|
G2 Let $A B C D$ be a convex quadrilateral with $\varangle D A C=\varangle B D C=36^{\circ}, \varangle C B D=18^{\circ}$ and $\varangle B A C=72^{\circ}$. If $P$ is the point of intersection of the diagonals $A C$ and $B D$, find the measure of $\varangle A P D$.
|
{"ground_truth": "108"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 40
|
numina_1.5_41
|
verifiable_math
|
NT1 Find all the pairs positive integers $(x, y)$ such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{[x, y]}+\frac{1}{(x, y)}=\frac{1}{2}
$$
where $(x, y)$ is the greatest common divisor of $x, y$ and $[x, y]$ is the least common multiple of $x, y$.
|
{"ground_truth": "(8,8),(9,24),(24,9),(5,20),(20,5),(12,15),(15,12),(8,12),(12,8),(6,12),(12,6)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 41
|
numina_1.5_42
|
verifiable_math
|
## A1
For any real number a, let $\lfloor a\rfloor$ denote the greatest integer not exceeding a. In positive real numbers solve the following equation
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=2014
$$
|
{"ground_truth": "1956"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 42
|
numina_1.5_43
|
verifiable_math
|
## C2
In a country with $n$ cities, all direct airlines are two-way. There are $r>2014$ routes between pairs of different cities that include no more than one intermediate stop (the direction of each route matters). Find the least possible $n$ and the least possible $r$ for that value of $n$.
|
{"ground_truth": "2016"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 43
|
numina_1.5_44
|
verifiable_math
|
## C3
For a given positive integer n, two players $A$ and B play the following game: Given is pile of $\boldsymbol{\Omega}$ stones. The players take turn alternatively with A going first. On each turn the player is allowed to take one stone, a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming perfect play, find the number of values for $S_{\infty}$, for which A cannot win.
|
{"ground_truth": "n-1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 44
|
numina_1.5_45
|
verifiable_math
|
## C4
Let $A=1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2014$ be the product of the numbers less or equal to 2014 that give remainder 1 when divided by 3 . Find the last non-zero digit of $A$.
|
{"ground_truth": "2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 45
|
numina_1.5_46
|
verifiable_math
|
## G3
Let $C D \perp A B(D \in A B), D M \perp A C(M \in A C)$ and $D N \perp B C(N \in B C)$ for an acute triangle ABC with area $S$. If $H_{1}$ and $H_{2}$ are the orthocentres of the triangles $M N C$ and MND respectively. Evaluate the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$.
|
{"ground_truth": "S"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 46
|
numina_1.5_47
|
verifiable_math
|
## N1
Each letter of the word OHRID corresponds to a different digit belonging to the set $(1,2,3,4,5)$. Decipher the equality $(O+H+R+I+D)^{2}:(O-H-R+I+D)=O^{H^{R^{I_{D}^{D}}}}$.
|
{"ground_truth": "O=5,H=2,R=1,I=3,D=4orO=5,H=2,R=1"}
|
{"source": "olympiads", "problem_type": "Logic and Puzzles"}
| 47
|
numina_1.5_48
|
verifiable_math
|
N3
Find the integer solutions of the equation
$$
x^{2}=y^{2}\left(x+y^{4}+2 y^{2}\right)
$$
|
{"ground_truth": "(x,y)=(0,0),(12,-2),(12,2),(-8,-2),(-8,2)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 48
|
numina_1.5_49
|
verifiable_math
|
## N6
Vukasin, Dimitrije, Dusan, Stefan and Filip asked their professor to guess a three consecutive positive integer numbers after they had told him these (true) sentences:
Vukasin: "Sum of the digits of one of them is a prime number. Sum of the digits of some of the other two is an even perfect number ( $n$ is perfect if $\sigma(n)=2 n$ ). Sum of the digits of the remaining number is equal to the number of its positive divisors."
Dimitrije:"Each of these three numbers has no more than two digits 1 in its decimal representation."
Dusan:"If we add 11 to one of them, we obtain a square of an integer."
Stefan:"Each of them has exactly one prime divisor less then 10."
Filip:"The 3 numbers are square-free."
Their professor gave the correct answer. Which numbers did he say?
|
{"ground_truth": "2013,2014,2015"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 49
|
numina_1.5_51
|
verifiable_math
|
A3. Let $A$ and $B$ be two non-empty subsets of $X=\{1,2, \ldots, 11\}$ with $A \cup B=X$. Let $P_{A}$ be the product of all elements of $A$ and let $P_{B}$ be the product of all elements of $B$. Find the minimum and maximum possible value of $P_{A}+P_{B}$ and find all possible equality cases.
|
{"ground_truth": "12636"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 50
|
numina_1.5_52
|
verifiable_math
|
C3. In a $5 \times 100$ table we have coloured black $n$ of its cells. Each of the 500 cells has at most two adjacent (by side) cells coloured black. Find the largest possible value of $n$.
|
{"ground_truth": "302"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 51
|
numina_1.5_53
|
verifiable_math
|
C4. We have a group of $n$ kids. For each pair of kids, at least one has sent a message to the other one. For each kid $A$, among the kids to whom $A$ has sent a message, exactly $25 \%$ have sent a message to $A$. How many possible two-digit values of $n$ are there?
|
{"ground_truth": "26"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 52
|
numina_1.5_54
|
verifiable_math
|
C5. An economist and a statistician play a game on a calculator which does only one operation. The calculator displays only positive integers and it is used in the following way: Denote by $n$ an integer that is shown on the calculator. A person types an integer, $m$, chosen from the set $\{1,2, \ldots, 99\}$ of the first 99 positive integers, and if $m \%$ of the number $n$ is again a positive integer, then the calculator displays $m \%$ of $n$. Otherwise, the calculator shows an error message and this operation is not allowed. The game consists of doing alternatively these operations and the player that cannot do the operation looses. How many numbers from $\{1,2, \ldots, 2019\}$ guarantee the winning strategy for the statistician, who plays second?
For example, if the calculator displays 1200, the economist can type 50 , giving the number 600 on the calculator, then the statistician can type 25 giving the number 150 . Now, for instance, the economist cannot type 75 as $75 \%$ of 150 is not a positive integer, but can choose 40 and the game continues until one of them cannot type an allowed number.
|
{"ground_truth": "931"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 53
|
numina_1.5_55
|
verifiable_math
|
N2. Find all triples $(p, q, r)$ of prime numbers such that all of the following numbers are integers
$$
\frac{p^{2}+2 q}{q+r}, \quad \frac{q^{2}+9 r}{r+p}, \quad \frac{r^{2}+3 p}{p+q}
$$
|
{"ground_truth": "(2,3,7)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 54
|
numina_1.5_56
|
verifiable_math
|
N4. Find all integers $x, y$ such that
$$
x^{3}(y+1)+y^{3}(x+1)=19
$$
|
{"ground_truth": "(2,1),(1,2),(-1,-20),(-20,-1)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 55
|
numina_1.5_57
|
verifiable_math
|
N5. Find all positive integers $x, y, z$ such that
$$
45^{x}-6^{y}=2019^{z}
$$
|
{"ground_truth": "(2,1,1)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 56
|
numina_1.5_58
|
verifiable_math
|
N6. Find all triples $(a, b, c)$ of nonnegative integers that satisfy
$$
a!+5^{b}=7^{c}
$$
|
{"ground_truth": "(,b,)\\in{(3,0,1),(1,2,1),(4,2,2)}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 57
|
numina_1.5_59
|
verifiable_math
|
N7. Find all perfect squares $n$ such that if the positive integer $a \geqslant 15$ is some divisor of $n$ then $a+15$ is a prime power.
|
{"ground_truth": "1,4,9,16,49,64,196"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 58
|
numina_1.5_60
|
verifiable_math
|
NT1 Solve in positive integers the equation $1005^{x}+2011^{y}=1006^{z}$.
|
{"ground_truth": "(2,1,2)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 59
|
numina_1.5_61
|
verifiable_math
|
NT2 Find all prime numbers $p$ such that there exist positive integers $x, y$ that satisfy the relation $x\left(y^{2}-p\right)+y\left(x^{2}-p\right)=5 p$.
|
{"ground_truth": "p\\in{2,3,7}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 60
|
numina_1.5_62
|
verifiable_math
|
NT3 Find all positive integers $n$ such that the equation $y^{2}+x y+3 x=n\left(x^{2}+x y+3 y\right)$ has at least a solution $(x, y)$ in positive integers.
|
{"ground_truth": "n\\in{1,3,4,9}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 61
|
numina_1.5_63
|
verifiable_math
|
NT4 Find all prime positive integers $p, q$ such that $2 p^{3}-q^{2}=2(p+q)^{2}$.
|
{"ground_truth": "(p,q)=(3,2)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 62
|
numina_1.5_64
|
verifiable_math
|
NT5 Find the least positive integer such that the sum of its digits is 2011 and the product of its digits is a power of 6 .
|
{"ground_truth": "34\\underbrace{88\\ldots8}_{93}\\underbrace{99\\ldots9}_{140}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 63
|
numina_1.5_65
|
verifiable_math
|
G2 Let $A D, B F$ and $C E$ be the altitudes of $\triangle A B C$. A line passing through $D$ and parallel to $A B$ intersects the line $E F$ at the point $G$. If $H$ is the orthocenter of $\triangle A B C$, find the angle $\widehat{C G H}$.
|
{"ground_truth": "90"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 64
|
numina_1.5_66
|
verifiable_math
|
G3 Let $A B C$ be a triangle in which ( $B L$ is the angle bisector of $\widehat{A B C}(L \in A C), A H$ is an altitude of $\triangle A B C(H \in B C)$ and $M$ is the midpoint of the side $[A B]$. It is known that the midpoints of the segments $[B L]$ and $[M H]$ coincides. Determine the internal angles of triangle $\triangle A B C$.
|
{"ground_truth": "60"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 65
|
numina_1.5_67
|
verifiable_math
|
G4 Point $D$ lies on the side $[B C]$ of $\triangle A B C$. The circumcenters of $\triangle A D C$ and $\triangle B A D$ are $O_{1}$ and $O_{2}$, respectively and $O_{1} O_{2} \| A B$. The orthocenter of $\triangle A D C$ is $H$ and $A H=O_{1} O_{2}$. Find the angles of $\triangle A B C$ if $2 m(<C)=3 m(<B)$.
|
{"ground_truth": "\\widehat{BAC}=105,\\widehat{ABC}=30,\\widehat{ACB}=45"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 66
|
numina_1.5_68
|
verifiable_math
|
G5 Inside the square $A B C D$, the equilateral triangle $\triangle A B E$ is constructed. Let $M$ be an interior point of the triangle $\triangle A B E$ such that $M B=\sqrt{2}, M C=\sqrt{6}, M D=\sqrt{5}$ and $M E=\sqrt{3}$. Find the area of the square $A B C D$.
|
{"ground_truth": "3+\\sqrt{6}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 67
|
numina_1.5_69
|
verifiable_math
|
NT2. Find all four digit numbers A such that
$$
\frac{1}{3} A+2000=\frac{2}{3} \bar{A}
$$
where $\bar{A}$ is the number with the same digits as $A$, but written in opposite order. (For example, $\overline{1234}=4321$.)
|
{"ground_truth": "2004"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 68
|
numina_1.5_70
|
verifiable_math
|
Problem A2. Determine all four digit numbers $\overline{a b c d}$ such that
$$
a(a+b+c+d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)\left(a^{6}+2 b^{6}+3 c^{6}+4 d^{6}\right)=\overline{a b c d}
$$
|
{"ground_truth": "2010"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 69
|
numina_1.5_71
|
verifiable_math
|
Problem A3. Find all pairs $(x, y)$ of real numbers such that $|x|+|y|=1340$ and $x^{3}+y^{3}+2010 x y=670^{3}$.
|
{"ground_truth": "(-670,-670),(1005,-335),(-335,1005)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 70
|
numina_1.5_72
|
verifiable_math
|
Problem G2. Consider a triangle $A B C$ and let $M$ be the midpoint of the side $B C$. Suppose $\angle M A C=\angle A B C$ and $\angle B A M=105^{\circ}$. Find the measure of $\angle A B C$.
|
{"ground_truth": "30"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 71
|
numina_1.5_73
|
verifiable_math
|
Problem C1. There are two piles of coins, each containing 2010 pieces. Two players A and B play a game taking turns (A plays first). At each turn, the player on play has to take one or more coins from one pile or exactly one coin from each pile. Whoever takes the last coin is the winner. Which player will win if they both play in the best possible way?
|
{"ground_truth": "Bwins"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 72
|
numina_1.5_74
|
verifiable_math
|
Problem N1. Find all positive integers $n$ such that $n 2^{n+1}+1$ is a perfect square.
|
{"ground_truth": "n=0n=3"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 73
|
numina_1.5_75
|
verifiable_math
|
Problem N2. Find all positive integers $n$ such that $36^{n}-6$ is a product of two or more consecutive positive integers.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 74
|
numina_1.5_76
|
verifiable_math
|
A3. Determine the number of pairs of integers $(m, n)$ such that
$$
\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}} \in \mathbb{Q}
$$
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 75
|
numina_1.5_77
|
verifiable_math
|
C1. Let $S_{n}$ be the sum of reciprocal values of non-zero digits of all positive integers up to (and including) $n$. For instance, $S_{13}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{2}+\frac{1}{1}+\frac{1}{3}$. Find the least positive integer $k$ making the number $k!\cdot S_{2016}$ an integer.
|
{"ground_truth": "7"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 76
|
numina_1.5_78
|
verifiable_math
|
C2. The natural numbers from 1 to 50 are written down on the blackboard. At least how many of them should be deleted, in order that the sum of any two of the remaining numbers is not a prime?
|
{"ground_truth": "25"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 77
|
numina_1.5_79
|
verifiable_math
|
C3. Consider any four pairwise distinct real numbers and write one of these numbers in each cell of a $5 \times 5$ array so that each number occurs exactly once in every $2 \times 2$ subarray. The sum over all entries of the array is called the total sum of that array. Determine the maximum number of distinct total sums that may be obtained in this way.
|
{"ground_truth": "60"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 78
|
numina_1.5_80
|
verifiable_math
|
C4. A splitting of a planar polygon is a finite set of triangles whose interiors are pairwise disjoint, and whose union is the polygon in question. Given an integer $n \geq 3$, determine the largest integer $m$ such that no planar $n$-gon splits into less than $m$ triangles.
|
{"ground_truth": "\\lceiln/3\\rceil"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 79
|
numina_1.5_81
|
verifiable_math
|
N1. Determine the largest positive integer $n$ that divides $p^{6}-1$ for all primes $p>7$.
|
{"ground_truth": "504"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 80
|
numina_1.5_82
|
verifiable_math
|
N2. Find the maximum number of natural numbers $x_{1}, x_{2}, \ldots, x_{m}$ satisfying the conditions:
a) No $x_{i}-x_{j}, 1 \leq i<j \leq m$ is divisible by 11 ; and
b) The sum $x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1}$ is divisible by 11 .
|
{"ground_truth": "10"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 81
|
numina_1.5_83
|
verifiable_math
|
N4. Find all triples of integers $(a, b, c)$ such that the number
$$
N=\frac{(a-b)(b-c)(c-a)}{2}+2
$$
is a power of 2016 .
|
{"ground_truth": "(,b,)=(k+2,k+1,k),k\\in\\mathbb{Z}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 82
|
numina_1.5_84
|
verifiable_math
|
N5. Determine all four-digit numbers $\overline{a b c d}$ such that
$$
(a+b)(a+c)(a+d)(b+c)(b+d)(c+d)=\overline{a b c d}
$$
|
{"ground_truth": "2016"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 83
|
numina_1.5_85
|
verifiable_math
|
A 1. Find all triples $(a, b, c)$ of real numbers such that the following system holds:
$$
\left\{\begin{array}{l}
a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \\
a^{2}+b^{2}+c^{2}=\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}
\end{array}\right.
$$
|
{"ground_truth": "(,b,)=(,\\frac{1}{},1),(,\\frac{1}{},-1)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 84
|
numina_1.5_86
|
verifiable_math
|
A 2. Consider the sequence $a_{1}, a_{2}, a_{3}, \ldots$ defined by $a_{1}=9$ and
$$
a_{n+1}=\frac{(n+5) a_{n}+22}{n+3}
$$
for $n \geqslant 1$.
Find all natural numbers $n$ for which $a_{n}$ is a perfect square of an integer.
|
{"ground_truth": "n=1orn=8"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 85
|
numina_1.5_87
|
verifiable_math
|
A 3. Find all triples of positive real numbers $(a, b, c)$ so that the expression
$$
M=\frac{(a+b)(b+c)(a+b+c)}{a b c}
$$
gets its least value.
|
{"ground_truth": "==\\sqrt[3]{\\frac{1+\\sqrt{5}}{2}},b=\\frac{1}{}"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 86
|
numina_1.5_88
|
verifiable_math
|
NT 2. Find all positive integers $a, b, c$ and $p$, where $p$ is a prime number, such that
$$
73 p^{2}+6=9 a^{2}+17 b^{2}+17 c^{2}
$$
|
{"ground_truth": "(,b,,p)\\in{(1,1,4,2),(1,4,1,2)}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 87
|
numina_1.5_89
|
verifiable_math
|
NT 3. Find the largest integer $k(k \geq 2)$, for which there exists an integer $n(n \geq k)$ such that from any collection of $n$ consecutive positive integers one can always choose $k$ numbers, which verify the following conditions:
1. each chosen number is not divisible by 6 , by 7 and by 8 ;
2. the positive difference of any two different chosen numbers is not divisible by at least one of the numbers 6,7 or 8 .
|
{"ground_truth": "108"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 88
|
numina_1.5_90
|
verifiable_math
|
NT 4. Find all prime numbers $p$ such that
$$
(x+y)^{19}-x^{19}-y^{19}
$$
is a multiple of $p$ for any positive integers $x, y$.
|
{"ground_truth": "2,3,7,19"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 89
|
numina_1.5_91
|
verifiable_math
|
NT 8. Find all pairs $(p, q)$ of prime numbers such that
$$
1+\frac{p^{q}-q^{p}}{p+q}
$$
is a prime number.
|
{"ground_truth": "(2,5)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 90
|
numina_1.5_92
|
verifiable_math
|
A 2. Find the maximum positive integer $k$ such that for any positive integers $m, n$ such that $m^{3}+n^{3}>$ $(m+n)^{2}$, we have
$$
m^{3}+n^{3} \geq(m+n)^{2}+k
$$
|
{"ground_truth": "10"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 91
|
numina_1.5_93
|
verifiable_math
|
A 4. Let $k>1, n>2018$ be positive integers, and let $n$ be odd. The nonzero rational numbers $x_{1}$, $x_{2}, \ldots, x_{n}$ are not all equal and satisfy
$$
x_{1}+\frac{k}{x_{2}}=x_{2}+\frac{k}{x_{3}}=x_{3}+\frac{k}{x_{4}}=\cdots=x_{n-1}+\frac{k}{x_{n}}=x_{n}+\frac{k}{x_{1}}
$$
Find:
a) the product $x_{1} x_{2} \ldots x_{n}$ as a function of $k$ and $n$
b) the least value of $k$, such that there exist $n, x_{1}, x_{2}, \ldots, x_{n}$ satisfying the given conditions.
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 92
|
numina_1.5_94
|
verifiable_math
|
A 7. Let $A$ be a set of positive integers with the following properties:
(a) If $n$ is an element of $A$ then $n \leqslant 2018$.
(b) If $S$ is a subset of $A$ with $|S|=3$ then there are two elements $n, m$ of $S$ with $|n-m| \geqslant \sqrt{n}+\sqrt{m}$.
What is the maximum number of elements that $A$ can have?
|
{"ground_truth": "88"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 93
|
numina_1.5_95
|
verifiable_math
|
C 1. A set $S$ is called neighbouring if it has the following two properties:
a) $S$ has exactly four elements
b) for every element $x$ of $S$, at least one of the numbers $x-1$ or $x+1$ belongs to $S$.
Find the number of all neighbouring subsets of the set $\{1,2, \ldots, n\}$.
|
{"ground_truth": "\\frac{(n-3)(n-2)}{2}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 94
|
numina_1.5_96
|
verifiable_math
|
C 2. A set $T$ of $n$ three-digit numbers has the following five properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
{"ground_truth": "5"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 95
|
numina_1.5_97
|
verifiable_math
|
NT 1. Find all the integers pairs $(x, y)$ which satisfy the equation
$$
x^{5}-y^{5}=16 x y
$$
|
{"ground_truth": "(x,y)=(0,0)or(-2,2)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 96
|
numina_1.5_98
|
verifiable_math
|
NT 2. Find all pairs $(m, n)$ of positive integers such that
$$
125 \cdot 2^{n}-3^{m}=271
$$
|
{"ground_truth": "(,n)=(6,3)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 97
|
numina_1.5_100
|
verifiable_math
|
A1 Determine all integers $a, b, c$ satisfying the identities:
$$
\begin{gathered}
a+b+c=15 \\
(a-3)^{3}+(b-5)^{3}+(c-7)^{3}=540
\end{gathered}
$$
|
{"ground_truth": "(,b,)\\in{(-1,0,16),(-2,1,16),(7,10,-2),(8,9,-2)}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 98
|
numina_1.5_101
|
verifiable_math
|
A2 Find the maximum value of $z+x$, if $(x, y, z, t)$ satisfies the conditions:
$$
\left\{\begin{array}{l}
x^{2}+y^{2}=4 \\
z^{2}+t^{2}=9 \\
x t+y z \geq 6
\end{array}\right.
$$
|
{"ground_truth": "\\sqrt{13}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 99
|
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 4