problem_id
stringlengths 12
21
| task_type
stringclasses 1
value | prompt
stringlengths 0
13.6k
| verification_info
stringlengths 20
1.24k
| metadata
stringclasses 89
values | __index_level_0__
int64 0
776k
|
|---|---|---|---|---|---|
numina_1.5_102
|
verifiable_math
|
A3 Find all values of the real parameter $a$, for which the system
$$
\left\{\begin{array}{c}
(|x|+|y|-2)^{2}=1 \\
y=a x+5
\end{array}\right.
$$
has exactly three solutions.
|
{"ground_truth": "=5or=-5"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 100
|
numina_1.5_103
|
verifiable_math
|
C2 Five players $(A, B, C, D, E)$ take part in a bridge tournament. Every two players must play (as partners) against every other two players. Any two given players can be partners not more than once per day. What is the least number of days needed for this tournament?
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 101
|
numina_1.5_104
|
verifiable_math
|
C3 a) In how many ways can we read the word SARAJEVO from the table below, if it is allowed to jump from cell to an adjacent cell (by vertex or a side) cell?
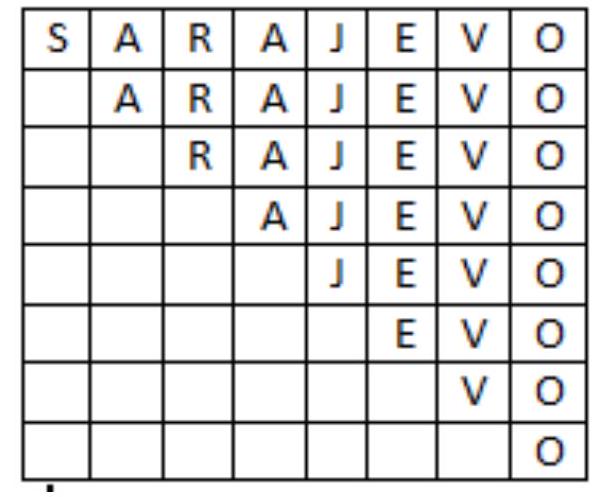
b) After the letter in one cell was deleted, only 525 ways to read the word SARAJEVO remained. Find all possible positions of that cell.
|
{"ground_truth": "750"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 102
|
numina_1.5_105
|
verifiable_math
|
G2 In a right trapezoid $A B C D(A B \| C D)$ the angle at vertex $B$ measures $75^{\circ}$. Point $H$ is the foot of the perpendicular from point $A$ to the line $B C$. If $B H=D C$ and $A D+A H=8$, find the area of $A B C D$.
|
{"ground_truth": "8"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 103
|
numina_1.5_106
|
verifiable_math
|
NT1 Determine all positive integer numbers $k$ for which the numbers $k+9$ are perfect squares and the only prime factors of $k$ are 2 and 3 .
|
{"ground_truth": "{16,27,72,216,432,2592}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 104
|
numina_1.5_107
|
verifiable_math
|
NT2 A group of $n>1$ pirates of different age owned total of 2009 coins. Initially each pirate (except for the youngest one) had one coin more than the next younger.
a) Find all possible values of $n$.
b) Every day a pirate was chosen. The chosen pirate gave a coin to each of the other pirates. If $n=7$, find the largest possible number of coins a pirate can have after several days.
|
{"ground_truth": "1994"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 105
|
numina_1.5_108
|
verifiable_math
|
NT3 Find all pairs $(x, y)$ of integers which satisfy the equation
$$
(x+y)^{2}\left(x^{2}+y^{2}\right)=2009^{2}
$$
|
{"ground_truth": "(40,9),(9,40),(-40,-9),(-9,-40)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 106
|
numina_1.5_109
|
verifiable_math
|
NT4 Determine all prime numbers $p_{1}, p_{2}, \ldots, p_{12}, p_{13}, p_{1} \leq p_{2} \leq \ldots \leq p_{12} \leq p_{13}$, such that
$$
p_{1}^{2}+p_{2}^{2}+\ldots+p_{12}^{2}=p_{13}^{2}
$$
and one of them is equal to $2 p_{1}+p_{9}$.
|
{"ground_truth": "(2,2,2,2,2,2,2,3,3,5,7,7,13),(2,2,2,2,2,2,2,3,3,5,7,13,17),(2,2,2,2,2,2,2,3,3,5,7,29,31)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 107
|
numina_1.5_110
|
verifiable_math
|
C2 Can we divide an equilateral triangle $\triangle A B C$ into 2011 small triangles using 122 straight lines? (there should be 2011 triangles that are not themselves divided into smaller parts and there should be no polygons which are not triangles)
|
{"ground_truth": "2011"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 108
|
numina_1.5_111
|
verifiable_math
|
C4 In a group of $n$ people, each one had a different ball. They performed a sequence of swaps; in each swap, two people swapped the ball they had at that moment. Each pair of people performed at least one swap. In the end each person had the ball he/she had at the start. Find the least possible number of swaps, if: $a$ ) $n=5$; b) $n=6$.
|
{"ground_truth": "16"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 109
|
numina_1.5_112
|
verifiable_math
|
C5 A set $S$ of natural numbers is called good, if for each element $x \in S, x$ does not divide the sum of the remaining numbers in $S$. Find the maximal possible number of elements of a good set which is a subset of the set $A=\{1,2,3, \ldots, 63\}$.
|
{"ground_truth": "61"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 110
|
numina_1.5_113
|
verifiable_math
|
C7 Consider a rectangle whose lengths of sides are natural numbers. If someone places as many squares as possible, each with area 3 , inside of the given rectangle, such that
the sides of the squares are parallel to the rectangle sides, then the maximal number of these squares fill exactly half of the area of the rectangle. Determine the dimensions of all rectangles with this property.
|
{"ground_truth": "(2,3);(3,4);(3,6);(3,8);(3,10);(3,12)"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 111
|
numina_1.5_114
|
verifiable_math
|
A2. Find all positive integers $x, y$ satisfying the equation
$$
9\left(x^{2}+y^{2}+1\right)+2(3 x y+2)=2005
$$
|
{"ground_truth": "(x,y)=(11,7)or(x,y)=(7,11)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 112
|
numina_1.5_115
|
verifiable_math
|
A3. Find the maximum value of the area of a triangle having side lengths $a, b, c$ with
$$
a^{2}+b^{2}+c^{2}=a^{3}+b^{3}+c^{3}
$$
|
{"ground_truth": "S\\leq\\frac{\\sqrt{3}}{4}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 113
|
numina_1.5_116
|
verifiable_math
|
A4. Find all the integer solutions of the equation
$$
9 x^{2} y^{2}+9 x y^{2}+6 x^{2} y+18 x y+x^{2}+2 y^{2}+5 x+7 y+6=0
$$
|
{"ground_truth": "(-2,0),(-3,0),(0,-2),(-1,2)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 114
|
numina_1.5_117
|
verifiable_math
|
A5. Solve the equation
$$
8 x^{3}+8 x^{2} y+8 x y^{2}+8 y^{3}=15\left(x^{2}+y^{2}+x y+1\right)
$$
in the set of integers.
|
{"ground_truth": "(x,y)=(1,2)(x,y)=(2,1)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 115
|
numina_1.5_118
|
verifiable_math
|
G3. Let $A B C D E F$ be a regular hexagon. The points $\mathrm{M}$ and $\mathrm{N}$ are internal points of the sides $\mathrm{DE}$ and $\mathrm{DC}$ respectively, such that $\angle A M N=90^{\circ}$ and $A N=\sqrt{2} \cdot C M$. Find the measure of the angle $\angle B A M$.
|
{"ground_truth": "75"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 116
|
numina_1.5_119
|
verifiable_math
|
G6. A point $O$ and the circles $k_{1}$ with center $O$ and radius $3, k_{2}$ with center $O$ and radius 5, are given. Let $A$ be a point on $k_{1}$ and $B$ be a point on $k_{2}$. If $A B C$ is equilateral triangle, find the maximum value of the distance $O C$.
|
{"ground_truth": "8"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 117
|
numina_1.5_120
|
verifiable_math
|
NT1. Find all the natural numbers $m$ and $n$, such that the square of $m$ minus the product of $n$ with $k$, is 2 , where the number $k$ is obtained from $n$ by writing 1 on the left of the decimal notation of $n$.
|
{"ground_truth": "=11,n=7"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 118
|
numina_1.5_121
|
verifiable_math
|
NT2. Find all natural numbers $n$ such that $5^{n}+12^{n}$ is perfect square.
|
{"ground_truth": "2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 119
|
numina_1.5_122
|
verifiable_math
|
NT4. Find all the three digit numbers $\overline{a b c}$ such that
$$
\overline{a b c}=a b c(a+b+c)
$$
|
{"ground_truth": "135144"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 120
|
numina_1.5_123
|
verifiable_math
|
C4. Let $p_{1}, p_{2}, \ldots, p_{2005}$ be different prime numbers. Let $\mathrm{S}$ be a set of natural numbers which elements have the property that their simple divisors are some of the numbers $p_{1}, p_{2}, \ldots, p_{2005}$ and product of any two elements from $\mathrm{S}$ is not perfect square.
What is the maximum number of elements in $\mathrm{S}$ ?
|
{"ground_truth": "2^{2005}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 121
|
numina_1.5_124
|
verifiable_math
|
A4 Let $x, y$ be positive real numbers such that $x^{3}+y^{3} \leq x^{2}+y^{2}$. Find the greatest possible value of the product $x y$.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 122
|
numina_1.5_125
|
verifiable_math
|
A5 Determine the positive integers $a, b$ such that $a^{2} b^{2}+208=4\{l c m[a ; b]+g c d(a ; b)\}^{2}$.
|
{"ground_truth": "(,b)\\in{(2,12);(4,6);(6,4);(12;2)}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 123
|
numina_1.5_127
|
verifiable_math
|
A1 If for the real numbers $x, y, z, k$ the following conditions are valid, $x \neq y \neq z \neq x$ and $x^{3}+y^{3}+k\left(x^{2}+y^{2}\right)=y^{3}+z^{3}+k\left(y^{2}+z^{2}\right)=z^{3}+x^{3}+k\left(z^{2}+x^{2}\right)=2008$, find the product $x y z$.
|
{"ground_truth": "xy1004"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 124
|
numina_1.5_128
|
verifiable_math
|
A2 Find all real numbers $a, b, c, d$ such that $a+b+c+d=20$ and $a b+a c+a d+b c+b d+c d=$ 150 .
|
{"ground_truth": "=b===5"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 125
|
numina_1.5_129
|
verifiable_math
|
A3 Let the real parameter $p$ be such that the system
$$
\left\{\begin{array}{l}
p\left(x^{2}-y^{2}\right)=\left(p^{2}-1\right) x y \\
|x-1|+|y|=1
\end{array}\right.
$$
has at least three different real solutions. Find $p$ and solve the system for that $p$.
|
{"ground_truth": "p=1orp=-1,0\\leqx\\leq1,withy=\\x"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 126
|
numina_1.5_130
|
verifiable_math
|
A4 Find all triples $(x, y, z)$ of real numbers that satisfy the system
$$
\left\{\begin{array}{l}
x+y+z=2008 \\
x^{2}+y^{2}+z^{2}=6024^{2} \\
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{2008}
\end{array}\right.
$$
|
{"ground_truth": "(2008,4016,-4016)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 127
|
numina_1.5_131
|
verifiable_math
|
A5 Find all triples $(x, y, z)$ of real positive numbers, which satisfy the system
$$
\left\{\begin{array}{l}
\frac{1}{x}+\frac{4}{y}+\frac{9}{z}=3 \\
x+y+z \leq 12
\end{array}\right.
$$
|
{"ground_truth": "(2,4,6)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 128
|
numina_1.5_132
|
verifiable_math
|
A9 Consider an integer $n \geq 4$ and a sequence of real numbers $x_{1}, x_{2}, x_{3}, \ldots, x_{n}$. An operation consists in eliminating all numbers not having the rank of the form $4 k+3$, thus leaving only the numbers $x_{3}, x_{7}, x_{11}, \ldots$ (for example, the sequence $4,5,9,3,6,6,1,8$ produces the sequence 9,1 . Upon the sequence $1,2,3, \ldots, 1024$ the operation is performed successively for 5 times. Show that at the end only 1 number remains and find this number.
|
{"ground_truth": "683"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 129
|
numina_1.5_133
|
verifiable_math
|
G3 The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 130
|
numina_1.5_134
|
verifiable_math
|
G7 Let $A B C$ be an isosceles triangle with $A C=B C$. The point $D$ lies on the side $A B$ such that the semicircle with diameter $[B D]$ and center $O$ is tangent to the side $A C$ in the point $P$ and intersects the side $B C$ at the point $Q$. The radius $O P$ intersects the chord $D Q$ at the point $E$ such that $5 \cdot P E=3 \cdot D E$. Find the ratio $\frac{A B}{B C}$.
|
{"ground_truth": "\\frac{6}{5}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 131
|
numina_1.5_135
|
verifiable_math
|
NT1 Find all the positive integers $x$ and $y$ that satisfy the equation
$$
x(x-y)=8 y-7
$$
|
{"ground_truth": "(x,y)=(63,56)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 132
|
numina_1.5_136
|
verifiable_math
|
NT3 Let $s(a)$ denote the sum of digits of a given positive integer $a$. The sequence $a_{1}, a_{2}, \ldots a_{n}, \ldots$ of positive integers is such that $a_{n+1}=a_{n}+s\left(a_{n}\right)$ for each positive integer $n$. Find the greatest possible $n$ for which it is possible to have $a_{n}=2008$.
|
{"ground_truth": "6"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 133
|
numina_1.5_137
|
verifiable_math
|
NT4 Find all integers $n$ such that $n^{4}+8 n+11$ is a product of two or more consecutive integers.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 134
|
numina_1.5_138
|
verifiable_math
|
NT6 Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, satisfying the following condition:
for every integer $n>1$, there exists a prime divisor $p$ of $n$ such that $f(n)=f\left(\frac{n}{p}\right)-f(p)$. If
$$
f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006
$$
determine the value of
$$
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right)
$$
|
{"ground_truth": "9"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 135
|
numina_1.5_139
|
verifiable_math
|
NT7 Determine the minimal prime number $p>3$ for which no natural number $n$ satisfies
$$
2^{n}+3^{n} \equiv 0(\bmod p)
$$
|
{"ground_truth": "19"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 136
|
numina_1.5_140
|
verifiable_math
|
NT8 Let $a, b, c, d, e, f$ are nonzero digits such that the natural numbers $\overline{a b c}, \overline{d e f}$ and $\overline{a b c d e f}$ are squares.
a) Prove that $\overline{a b c d e f}$ can be represented in two different ways as a sum of three squares of natural numbers.
b) Give an example of such a number.
|
{"ground_truth": "225625=475^{2}=450^{2}+150^{2}+25^{2}=270^{2}+390^{2}+25^{2}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 137
|
numina_1.5_141
|
verifiable_math
|
NT9 Let $p$ be a prime number. Find all positive integers $a$ and $b$ such that:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}
$$
and
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}
$$
are integers.
|
{"ground_truth": "(,b)={(1,1),(2,2),(p,p),(2p,2p),(5,25),(6,18),(18,6),(25,5),(30,150),(150,30)}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 138
|
numina_1.5_142
|
verifiable_math
|
NT11 Determine the greatest number with $n$ digits in the decimal representation which is divisible by 429 and has the sum of all digits less than or equal to 11 .
|
{"ground_truth": "30030000\\ldots"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 139
|
numina_1.5_143
|
verifiable_math
|
NT12 Solve the equation $\frac{p}{q}-\frac{4}{r+1}=1$ in prime numbers.
|
{"ground_truth": "(p,q,r)=(3,2,7),"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 140
|
numina_1.5_144
|
verifiable_math
|
COM 1. In a group of 60 students: 40 speak English; 30 speak French; 8 speak all the three languages; the number of students that speak English and French but not German is equal to "the sum of the number of students that speak English and German but not French plus the number of students that speak French and German but not English; and the number of students that speak at least 2 of those fanguages is 28 . How many students speak:
a) German;
b) only English;
c) only German?
|
{"ground_truth": "26"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 141
|
numina_1.5_145
|
verifiable_math
|
COM 2 Natural numbers 1,2,3, .., 2003 are written in an arbitrary sequence $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$. Let $b_{1}=1 a_{1}, b_{2}=2 a_{2}, b_{3}=3 a_{3}, \ldots, b_{2003}=2003 a_{2003}$, and $B$ be the maximum of the numbers $b_{1}, b_{2}, b_{3}, \ldots, b_{2003}$.
a) If $a_{1}=2003, a_{2}=2002, a_{3}=2001, \ldots, a_{2002}=2, a_{2003}=1$, find the value of $B$.
b) Prove that $B \geq 1002^{2}$.
|
{"ground_truth": "1002^2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 142
|
numina_1.5_146
|
verifiable_math
|
87.3. Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 143
|
numina_1.5_147
|
verifiable_math
|
88.1. The positive integer $n$ has the following property: if the three last digits of $n$ are removed, the number $\sqrt[3]{n}$ remains. Find $n$.
|
{"ground_truth": "32768"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 144
|
numina_1.5_148
|
verifiable_math
|
89.2. Three sides of a tetrahedron are right-angled triangles having the right angle at their common vertex. The areas of these sides are $A, B$, and $C$. Find the total surface area of the tetrahedron.
|
{"ground_truth": "A+B+C+\\sqrt{A^{2}+B^{2}+C^{2}}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 145
|
numina_1.5_150
|
verifiable_math
|
91.1. Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
{"ground_truth": "12"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 146
|
numina_1.5_151
|
verifiable_math
|
92.1. Determine all real numbers $x>1, y>1$, and $z>1$, satisfying the equation
$$
\begin{aligned}
x+y+z+\frac{3}{x-1} & +\frac{3}{y-1}+\frac{3}{z-1} \\
& =2(\sqrt{x+2}+\sqrt{y+2}+\sqrt{z+2})
\end{aligned}
$$
|
{"ground_truth": "\\frac{3+\\sqrt{13}}{2}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 147
|
numina_1.5_152
|
verifiable_math
|
92.4. Peter has many squares of equal side. Some of the squares are black, some are white. Peter wants to assemble a big square, with side equal to $n$ sides of the small squares, so that the big square has no rectangle formed by the small squares such that all the squares in the vertices of the rectangle are of equal colour. How big a square is Peter able to assemble?
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 148
|
numina_1.5_153
|
verifiable_math
|
93.1. Let $F$ be an increasing real function defined for all $x, 0 \leq x \leq 1$, satisfying the conditions
$$
\begin{aligned}
& F\left(\frac{x}{3}\right)=\frac{F(x)}{2} \\
& F(1-x)=1-F(x)
\end{aligned}
$$
Determine $F\left(\frac{173}{1993}\right)$ and $F\left(\frac{1}{13}\right)$.
|
{"ground_truth": "\\frac{3}{16},\\frac{1}{7}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 149
|
numina_1.5_154
|
verifiable_math
|
93.3. Find all solutions of the system of equations
$$
\left\{\begin{aligned}
s(x)+s(y) & =x \\
x+y+s(z) & =z \\
s(x)+s(y)+s(z) & =y-4
\end{aligned}\right.
$$
where $x, y$, and $z$ are positive integers, and $s(x), s(y)$, and $s(z)$ are the numbers of digits in the decimal representations of $x, y$, and $z$, respectively.
|
{"ground_truth": "(2,8,12)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 150
|
numina_1.5_155
|
verifiable_math
|
94.4. Determine all positive integers $n<200$, such that $n^{2}+(n+1)^{2}$ is the square of an integer.
|
{"ground_truth": "20,3,119"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 151
|
numina_1.5_156
|
verifiable_math
|
95.2. Messages are coded using sequences consisting of zeroes and ones only. Only sequences with at most two consecutive ones or zeroes are allowed. (For instance the sequence 011001 is allowed, but 011101 is not.) Determine the number of sequences consisting of exactly 12 numbers.
|
{"ground_truth": "466"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 152
|
numina_1.5_157
|
verifiable_math
|
96.2. Determine all real numbers $x$, such that
$$
x^{n}+x^{-n}
$$
is an integer for all integers $n$.
|
{"ground_truth": "\\frac{}{2}\\"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 153
|
numina_1.5_158
|
verifiable_math
|
97.1. Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
{"ground_truth": "9"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 154
|
numina_1.5_159
|
verifiable_math
|
97.3. Let $A, B, C$, and $D$ be four different points in the plane. Three of the line segments $A B, A C, A D, B C, B D$, and $C D$ have length a. The other three have length $b$, where $b>a$. Determine all possible values of the quotient $\frac{b}{a}$.
|
{"ground_truth": "\\frac{\\sqrt{5}+1}{2}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 155
|
numina_1.5_160
|
verifiable_math
|
98.1. Determine all functions $f$ defined in the set of rational numbers and taking their values in the same set such that the equation $f(x+y)+f(x-y)=2 f(x)+2 f(y)$ holds for all rational numbers $x$ and $y$.
|
{"ground_truth": "f(x)=^{2}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 156
|
numina_1.5_162
|
verifiable_math
|
99.1. The function $f$ is defined for non-negative integers and satisfies the condition
$$
f(n)= \begin{cases}f(f(n+11)), & \text { if } n \leq 1999 \\ n-5, & \text { if } n>1999\end{cases}
$$
Find all solutions of the equation $f(n)=1999$.
|
{"ground_truth": "1999=f(6n),ifonlyifn=1,2,\\ldots,334"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 157
|
numina_1.5_163
|
verifiable_math
|
99.2. Consider 7-gons inscribed in a circle such that all sides of the 7-gon are of different length. Determine the maximal number of $120^{\circ}$ angles in this kind of a 7-gon.
|
{"ground_truth": "2"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 158
|
numina_1.5_164
|
verifiable_math
|
00.1. In how many ways can the number 2000 be written as a sum of three positive, not necessarily different integers? (Sums like $1+2+3$ and $3+1+2$ etc. are the same.)
|
{"ground_truth": "333333"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 159
|
numina_1.5_165
|
verifiable_math
|
00.2. The persons $P_{1}, P_{1}, \ldots, P_{n-1}, P_{n}$ sit around a table, in this order, and each one of them has a number of coins. In the start, $P_{1}$ has one coin more than $P_{2}, P_{2}$ has one coin more than $P_{3}$, etc., up to $P_{n-1}$ who has one coin more than $P_{n}$. Now $P_{1}$ gives one coin to $P_{2}$, who in turn gives two coins to $P_{3}$ etc., up to $P_{n}$ who gives $n$ coins to $P_{1}$. Now the process continues in the same way: $P_{1}$ gives $n+1$ coins to $P_{2}, P_{2}$ gives $n+2$ coins to $P_{3}$; in this way the transactions go on until someone has not enough coins, i.e. a person no more can give away one coin more than he just received. At the moment when the process comes to an end in this manner, it turns out that there are to neighbours at the table such that one of them has exactly five times as many coins as the other. Determine the number of persons and the number of coins circulating around the table.
|
{"ground_truth": "6or63"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 160
|
numina_1.5_166
|
verifiable_math
|
01.3. Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
{"ground_truth": "0"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 161
|
numina_1.5_167
|
verifiable_math
|
02.2. In two bowls there are in total $N$ balls, numbered from 1 to $N$. One ball is moved from one of the bowls to the other. The average of the numbers in the bowls is increased in both of the bowls by the same amount, $x$. Determine the largest possible value of $x$.
|
{"ground_truth": "\\frac{1}{2}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 162
|
numina_1.5_168
|
verifiable_math
|
02.4. Eva, Per and Anna play with their pocket calculators. They choose different integers and check, whether or not they are divisible by 11. They only look at nine-digit numbers consisting of all the digits 1, 2, .., 9. Anna claims that the probability of such a number to be a multiple of 11 is exactly 1/11. Eva has a different opinion: she thinks the probability is less than $1 / 11$. Per thinks the probability is more than $1 / 11$. Who is correct?
|
{"ground_truth": "\\frac{11}{126}<\\frac{1}{11}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 163
|
numina_1.5_169
|
verifiable_math
|
03.2. Find all triples of integers $(x, y, z)$ satisfying
$$
x^{3}+y^{3}+z^{3}-3 x y z=2003
$$
|
{"ground_truth": "(668,668,667)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 164
|
numina_1.5_170
|
verifiable_math
|
03.4. Let $\mathbb{R}^{*}=\mathbb{R} \backslash\{0\}$ be the set of non-zero real numbers. Find all functions $f: \mathbb{R}^{*} \rightarrow \mathbb{R}^{*}$ satisfying
$$
f(x)+f(y)=f(x y f(x+y))
$$
for $x, y \in \mathbb{R}^{*}$ and $x+y \neq 0$.
|
{"ground_truth": "f(x)=\\frac{1}{x}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 165
|
numina_1.5_171
|
verifiable_math
|
04.1. 27 balls, labelled by numbers from 1 to 27, are in a red, blue or yellow bowl. Find the possible numbers of balls in the red bowl, if the averages of the labels in the red, blue, and yellow bowl are 15, 3 ja 18, respectively.
|
{"ground_truth": "21,16,11"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 166
|
numina_1.5_172
|
verifiable_math
|
05.1. Find all positive integers $k$ such that the product of the digits of $k$, in the decimal system, equals
$$
\frac{25}{8} k-211
$$
|
{"ground_truth": "7288"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 167
|
numina_1.5_173
|
verifiable_math
|
06.2. The real numbers $x, y$ and $z$ are not all equal and satisfy
$$
x+\frac{1}{y}=y+\frac{1}{z}=z+\frac{1}{x}=k
$$
Determine all possible values of $k$.
|
{"ground_truth": "\\1"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 168
|
numina_1.5_174
|
verifiable_math
|
06.3. A sequence of positive integers $\left\{a_{n}\right\}$ is given by
$$
a_{0}=m \quad \text { and } \quad a_{n+1}=a_{n}^{5}+487
$$
for all $n \geq 0$. Determine all values of $m$ for which the sequence contains as many square numbers as possible.
|
{"ground_truth": "9"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 169
|
numina_1.5_175
|
verifiable_math
|
07.1. Find one solution in positive integers to the equation
$$
x^{2}-2 x-2007 y^{2}=0
$$
|
{"ground_truth": "(225,5)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 170
|
numina_1.5_176
|
verifiable_math
|
08.1. Determine all real numbers $A, B$ and $C$ such that there exists a real function $f$ that satisfies
$$
f(x+f(y))=A x+B y+C
$$
for all real $x$ and $y$.
|
{"ground_truth": "(A,B,C)=(,^2,)where\\neq-1arbitrary,or(A,B,C)=(-1,1,0)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 171
|
numina_1.5_177
|
verifiable_math
|
08.2. Assume that $n \geq 3$ people with different names sit around a round table. We call any unordered pair of them, say $M$ and $N$, dominating, if
(i) $M$ and $N$ do not sit on adjacent seats, and
(ii) on one (or both) of the arcs connecting $M$ and $N$ along the table edge, all people have names that come alphabetically after the names of $M$ and $N$.
Determine the minimal number of dominating pairs.
|
{"ground_truth": "n-3"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 172
|
numina_1.5_178
|
verifiable_math
|
09.2. On a faded piece of paper it is possible, with some effort, to discern the following:
$$
\left(x^{2}+x+a\right)\left(x^{15}-\ldots\right)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
$$
Some parts have got lost, partly the constant term of the first factor of the left side, partly the main part of the other factor. It would be possible to restore the polynomial forming the other factor, but we restrict ourselves to asking the question: What is the value of the constant term a? We assume that all polynomials in the statement above have only integer coefficients.
|
{"ground_truth": "2"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 173
|
numina_1.5_179
|
verifiable_math
|
10.3. Laura has 2010 lamps connected with 2010 buttons in front of her. For each button, she wants to know the corresponding lamp. In order to do this, she observes which lamps are lit when Richard presses a selection of buttons. (Not pressing anything is also a possible selection.) Richard always presses the buttons simultaneously, so the lamps are lit simultaneously, too.
a) If Richard chooses the buttons to be pressed, what is the maximum number of different combinations of buttons he can press until Laura can assign the buttons to the lamps correctly?
b) Supposing that Laura will choose the combinations of buttons to be pressed, what is the minimum number of attempts she has to do until she is able to associate the buttons with the lamps in a correct way?
|
{"ground_truth": "11"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 174
|
numina_1.5_180
|
verifiable_math
|
10.4. A positive integer is called simple if its ordinary decimal representation consists entirely of zeroes and ones. Find the least positive integer $k$ such that each positive integer $n$ can be written as $n=a_{1} \pm a_{2} \pm a_{3} \pm \cdots \pm a_{k}$, where $a_{1}, \ldots, a_{k}$ are simple.
|
{"ground_truth": "9"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 175
|
numina_1.5_181
|
verifiable_math
|
## Problem 2
Let $A B C D$ be a cyclic quadrilateral satisfying $A B=A D$ and $A B+B C=C D$.
Determine $\angle C D A$.
|
{"ground_truth": "60"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 176
|
numina_1.5_182
|
verifiable_math
|
## Problem 3
Find all $a \in \mathbb{R}$ for which there exists a function $f: \mathbb{R} \rightarrow \mathbb{R}$, such that
(i) $f(f(x))=f(x)+x$, for all $x \in \mathbb{R}$,
(ii) $f(f(x)-x)=f(x)+$ ax, for all $x \in \mathbb{R}$.
|
{"ground_truth": "\\frac{1\\\\sqrt{5}}{2}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 177
|
numina_1.5_183
|
verifiable_math
|
## Problem 4
King George has decided to connect the 1680 islands in his kingdom by bridges. Unfortunately the rebel movement will destroy two bridges after all the bridges have been built, but not two bridges from the same island.
What is the minimal number of bridges the King has to build in order to make sure that it is still possible to travel by bridges between any two of the 1680 islands after the rebel movement has destroyed two bridges?
|
{"ground_truth": "2016"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 178
|
numina_1.5_184
|
verifiable_math
|
## Problem 1
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(f(x) f(1-x))=f(x) \quad \text { and } \quad f(f(x))=1-f(x)
$$
for all real $x$.
|
{"ground_truth": "f(x)=\\frac{1}{2}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 179
|
numina_1.5_186
|
verifiable_math
|
Problem 3. Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \ldots, x_{n}$ (not necessarily different), with $1 \leq x_{k} \leq n, 1 \leq k \leq n$, and such that
$$
x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}, \quad \text { and } \quad x_{1} x_{2} \cdots x_{n}=n!
$$
but $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} \neq\{1,2, \ldots, n\}$.
|
{"ground_truth": "9"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 180
|
numina_1.5_187
|
verifiable_math
|
Problem 4. The number 1 is written on the blackboard. After that a sequence of numbers is created as follows: at each step each number $a$ on the blackboard is replaced by the numbers $a-1$ and $a+1$; if the number 0 occurs, it is erased immediately; if a number occurs more than once, all its occurrences are left on the blackboard. Thus the blackboard will show 1 after 0 steps; 2 after 1 step; 1,3 after 2 steps; 2, 2, 4 after 3 steps, and so on. How many numbers will there be on the blackboard after $n$ steps?
|
{"ground_truth": "\\binom{n}{\\lfloor\\frac{n}{2}\\rfloor}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 181
|
numina_1.5_188
|
verifiable_math
|
## Problem 2.
Find the primes $p, q, r$, given that one of the numbers $p q r$ and $p+q+r$ is 101 times the other.
|
{"ground_truth": "{2,101,103}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 182
|
numina_1.5_189
|
verifiable_math
|
## Problem 4.
An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:
(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.
(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.
How many different permutations of the volumes can be obtained by using these two operations repeatedly?
|
{"ground_truth": "(1000!)^2"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 183
|
numina_1.5_190
|
verifiable_math
|
Problem 2. In a football tournament there are $n$ teams, with $n \geq 4$, and each pair of teams meets exactly once. Suppose that, at the end of the tournament, the final scores form an arithmetic sequence where each team scores 1 more point than the following team on the scoreboard. Determine the maximum possible score of the lowest scoring team, assuming usual scoring for football games (where the winner of a game gets 3 points, the loser 0 points, and if there is a tie both teams get 1 point).
|
{"ground_truth": "n-2"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 184
|
numina_1.5_191
|
verifiable_math
|
LIV OM - II - Task 3
Given is the polynomial $ W(x) = x^4 - 3x^3 + 5x^2 - 9x $. Determine all pairs of different integers $ a $, $ b $ satisfying the equation
|
{"ground_truth": "(-1,0),(0,-1),(1,2),(2,1)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 185
|
numina_1.5_192
|
verifiable_math
|
XXIV OM - I - Problem 8
Find a polynomial with integer coefficients of the lowest possible degree, for which $ \sqrt{2} + \sqrt{3} $ is a root.
|
{"ground_truth": "x^4-10x^2+1"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 186
|
numina_1.5_193
|
verifiable_math
|
XLVII OM - I - Problem 2
A palindromic number is defined as a natural number whose decimal representation read from left to right is the same as when read from right to left. Let $ (x_n) $ be the increasing sequence of all palindromic numbers. Determine all prime numbers that are divisors of at least one of the differences $ x_{n+1}-x_n $.
|
{"ground_truth": "2,5,11"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 187
|
numina_1.5_194
|
verifiable_math
|
VI OM - I - Problem 9
Present the polynomial $ x^4 + x^3 + x^2 + x + 1 $ as the difference of squares of two polynomials of different degrees with real coefficients.
|
{"ground_truth": "x^4+x^3+x^2+x+1=(x^2+\\frac{1}{2}x+1)^2-(\\frac{1}{2}x)^2"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 188
|
numina_1.5_195
|
verifiable_math
|
XLVI OM - I - Problem 11
Given are natural numbers $ n > m > 1 $. From the set $ \{1,2, \ldots ,n\} $, we draw $ m $ numbers without replacement. Calculate the expected value of the difference between the largest and the smallest drawn number.
|
{"ground_truth": "\\frac{(n-1)}{n-+1}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 189
|
numina_1.5_196
|
verifiable_math
|
Given an integer $ c \geq 1 $. To each subset $ A $ of the set $ \{1,2, \ldots ,n\} $, we assign a number $ w(A) $ from the set $ \{1,2, \ldots ,c\} $ such that the following condition is satisfied:
Let $ a(n) $ be the number of such assignments. Calculate $ \lim_{n\to \infty}\sqrt[n]{a(n)} $.
Note: $ \min(x,y) $ is the smaller of the numbers $ x $, $ y $.
|
{"ground_truth": "c"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 190
|
numina_1.5_197
|
verifiable_math
|
LV OM - III - Task 3
In a certain tournament, $ n $ players participated $ (n \geq 3) $. Each played against each other exactly once, and there were no draws. A three-element set of players is called a draw triplet if the players can be numbered in such a way that the first won against the second, the second against the third, and the third against the first. Determine the maximum number of draw triplets that could have appeared in the tournament.
|
{"ground_truth": "\\frac{1}{24}n(n^2-1)"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 191
|
numina_1.5_198
|
verifiable_math
|
XXIV OM - I - Problem 10
Find the smallest natural number $ n > 1 $ with the following property: there exists a set $ Z $ consisting of $ n $ points in the plane such that every line $ AB $ ($ A, B \in Z $) is parallel to some other line $ CD $ ($ C, D \in Z $).
|
{"ground_truth": "5"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 192
|
numina_1.5_200
|
verifiable_math
|
XXV - I - Task 1
During World War I, a battle took place near a certain castle. One of the shells destroyed a statue of a knight with a spear standing at the entrance to the castle. This happened on the last day of the month. The product of the day of the month, the month number, the length of the spear expressed in feet, half the age of the battery commander firing at the castle expressed in years, and half the time the statue stood expressed in years equals 451,066. In which year was the statue erected?
|
{"ground_truth": "1714"}
|
{"source": "olympiads", "problem_type": "Logic and Puzzles"}
| 193
|
numina_1.5_202
|
verifiable_math
|
XXI OM - III - Task 1
Diameter $ \overline{AB} $ divides the circle into two semicircles. On one semicircle, n points $ P_1 P_2, \ldots, P_n $ are chosen such that $ P_1 $ lies between $ A $ and $ P_2 $, $ P_2 $ lies between $ P_1 $ and $ P_3 $, $ \ldots $, $ P_n $ lies between $ P_{n-1} $ and $ B $. How should point $ C $ be chosen on the other semicircle so that the sum of the areas of triangles $ CP_1P_2, CP_2P_3, CP_3P_4, \ldots, CP_{n-1}P_n $ is maximized?
|
{"ground_truth": "C"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 194
|
numina_1.5_204
|
verifiable_math
|
LVI OM - I - Problem 10
Among all subsets of a fixed $ n $-element set $ X $, we sequentially draw with replacement three sets $ A $, $ B $, $ C $. Each time, the probability of drawing any of the $ 2^n $ subsets of set $ X $ is equally likely. Determine the most probable number of elements in the set $ A\cap B\cap C $.
|
{"ground_truth": "[\\frac{1}{8}(n+1)]"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 195
|
numina_1.5_205
|
verifiable_math
|
XXII OM - I - Problem 10
Given is a table with $ n $ rows and $ n $ columns. The number located in the $ m $-th column and $ k $-th row is equal to $ n(k - 1) + m $. How should $ n $ numbers be chosen, one from each row and each column, so that the product of these numbers is the largest?
|
{"ground_truth": "a_{1n}a_{2n-1}\\ldotsa_{n1}=n(2n-1)(3n-2)(4n-3)\\ldots(n^2-(n-1))"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 196
|
numina_1.5_207
|
verifiable_math
|
V OM - I - Problem 7
In the plane, a line $ p $ and points $ A $ and $ B $ are given. Find a point $ M $ on the line $ p $ such that the sum of the squares $ AM^2 + BM^2 $ is minimized.
|
{"ground_truth": "M"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 197
|
numina_1.5_208
|
verifiable_math
|
XXIX OM - I - Problem 12
Determine the least upper bound of such numbers $ \alpha \leq \frac{\pi}{2} $, that every acute angle $ MON $ of measure $ \alpha $ and every triangle $ T $ on the plane have the following property. There exists a triangle $ ABC $ isometric to $ T $ such that the side $ \overline{AB} $ is parallel to $ OM $ and the lines perpendicular to $ ON $ and passing through the centroids of triangles $ ABC $ and $ ABC' $ respectively intersect the segment $ \overline{AB} $; $ C' $ is the reflection of vertex $ C $ across the perpendicular bisector of side $ \overline{AB} $.
Note. Physically, the problem means: What should be the angle of inclination of an inclined plane so that for any triangle, one can choose a certain side such that the triangle, placed with this side on the inclined plane, will not tip over.
|
{"ground_truth": "\\frac{\\pi}{3}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 198
|
numina_1.5_210
|
verifiable_math
|
LVII OM - I - Problem 4
Participants in a mathematics competition solved six problems, each graded with one of the scores 6, 5, 2, 0. It turned out that
for every pair of participants $ A, B $, there are two problems such that in each of them $ A $ received a different score than $ B $.
Determine the maximum number of participants for which such a situation is possible.
|
{"ground_truth": "1024"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 199
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.