problem_id
stringlengths 12
21
| task_type
stringclasses 1
value | prompt
stringlengths 0
13.6k
| verification_info
stringlengths 20
1.24k
| metadata
stringclasses 89
values | __index_level_0__
int64 0
776k
|
|---|---|---|---|---|---|
numina_1.5_334
|
verifiable_math
|
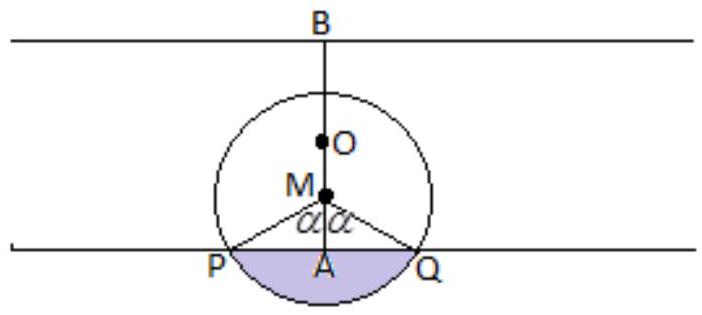
V OM - I - Task 11
Given are two intersecting lines $ a $ and $ b $. Find the geometric locus of point $ M $ having the property that the distance between the orthogonal projections of point $ M $ on lines $ a $ and $ b $ is constant, equal to a given segment $ d $.
|
{"ground_truth": "The\\geometric\\locus\\is\\the\\circle\\with\\center\\O\\\\radius\\\\frac{}{\\sin\\alpha}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 300
|
numina_1.5_336
|
verifiable_math
|
X OM - I - Task 8
The sides of a triangle are the medians of another triangle. Calculate the ratio of the areas of both triangles. Can a triangle be constructed from the medians of any triangle?
|
{"ground_truth": "\\frac{3}{4}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 301
|
numina_1.5_337
|
verifiable_math
|
XXV - I - Problem 11
Let $ X_n $ and $ Y_n $ be independent random variables with the same distribution $ \left{ \left(\frac{k}{2^n}, \frac{1}{2^n}\right) : k = 0, 1, \ldots, 2^n-1\right} $. Denote by $ p_n $ the probability of the event that there exists a real number $ t $ satisfying the equation $ t^2 + X_n \cdot t + Y_n = 0 $. Calculate $ \lim_{n\to\infty} p_n $.
|
{"ground_truth": "\\frac{1}{12}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 302
|
numina_1.5_338
|
verifiable_math
|
XXXVIII OM - II - Task 1
From an urn containing one ball marked with the number 1, two balls marked with the number 2, ..., $ n $ balls marked with the number $ n $, we draw two balls without replacement. We assume that drawing each ball from the urn is equally probable. Calculate the probability that both drawn balls have the same number.
|
{"ground_truth": "\\frac{4}{3(n+2)}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 303
|
numina_1.5_339
|
verifiable_math
|
LX OM - I - Task 5
For each integer $ n \geqslant 1 $, determine the largest possible number of different subsets of the set $ \{1,2,3, \cdots,n\} $ with the following property: Any two of these subsets are either disjoint or one is contained in the other.
|
{"ground_truth": "2n"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 304
|
numina_1.5_340
|
verifiable_math
|
LX OM - III - Problem 6
Let $ n \geqslant $ 3 be a natural number. The sequence of non-negative numbers
$ (c_0,c_1,\cdots ,c_n) $ satisfies the condition
for all $ p, r, s, t \geqslant 0 $ such that $ p + r + s + t = n $. Determine all possible
values of $ c_2 $, if $ c_1 =1 $.
|
{"ground_truth": "2\\cos(\\pi/n)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 305
|
numina_1.5_342
|
verifiable_math
|
X OM - II - Task 2
Under what relationship between the sides of a triangle is it similar to the triangle formed by its medians?
|
{"ground_truth": "^2=2b^2-^2"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 306
|
numina_1.5_343
|
verifiable_math
|
XIX OM - II - Problem 5
Tetrahedra $ABCD$ and $A_1B_1C_1D_1$ are positioned such that the midpoints of segments $AA_1$, $BB_1$, $CC_1$, $DD_1$ are the centroids of triangles $BCD$, $ACD$, $ABD$, and $ABC$, respectively. In what ratio are the volumes of these tetrahedra?
|
{"ground_truth": "(\\frac{5}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 307
|
numina_1.5_344
|
verifiable_math
|
XXVIII - I - Problem 11
From the numbers $ 1, 2, \ldots, n $, we choose one, with each of them being equally likely. Let $ p_n $ be the probability of the event that in the decimal representation of the chosen number, all digits: $ 0, 1, \ldots, 9 $ appear. Calculate $ \lim_{n\to \infty} p_n $.
|
{"ground_truth": "0"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 308
|
numina_1.5_346
|
verifiable_math
|
XLII OM - I - Problem 12
For any natural number $ n $, consider the rectangular prism $ K_n $ with edge lengths $ 1,1,n $ and the set $ R_n $ consisting of $ 4n+1 $ points: the vertices of the rectangular prism $ K_n $ and the points dividing its longer edges into unit segments. We randomly select three different points from the set $ R_n $. Let $ p_n $ be the probability that the selected points are the vertices of an obtuse triangle. Calculate $ \lim_{n\to \infty} p_n $.
Note: Three collinear points do not form a triangle.
|
{"ground_truth": "\\frac{15}{16}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 309
|
numina_1.5_347
|
verifiable_math
|
XIII OM - II - Task 6
Find a three-digit number with the property that the number represented by these digits and in the same order, but in a different base of numeration than $ 10 $, is twice as large as the given number.
|
{"ground_truth": "145,150,295"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 310
|
numina_1.5_349
|
verifiable_math
|
XXXII - II - Task 4
Given are natural numbers $ k, n $. We define inductively two sequences of numbers $ (a_j) $ and $ (r_j) $ as follows:
First step: divide $ k $ by $ n $ and obtain the quotient $ a_1 $ and the remainder $ r_1 $,
j-th step: divide $ k + r_{j-1} $ by $ n $ and obtain the quotient $ a_j $ and the remainder $ r_j $. Calculate the sum $ a_1 + \ldots + a_n $.
|
{"ground_truth": "k"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 311
|
numina_1.5_350
|
verifiable_math
|
XXXIX OM - I - Problem 8
For a given cube with edge length 1, find the set of segments with a total length not exceeding $1 + 3\sqrt{3}$, having the property that any two vertices of the cube are the endpoints of some broken line composed of segments from this set.
|
{"ground_truth": "1+3\\sqrt{3}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 312
|
numina_1.5_353
|
verifiable_math
|
XXII OM - III - Problem 5
Find the largest integer $ A $ such that for every permutation of the set of natural numbers not greater than 100, the sum of some 10 consecutive terms is at least $ A $.
|
{"ground_truth": "505"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 313
|
numina_1.5_354
|
verifiable_math
|
XXXIII OM - I - Problem 9
In a chessboard created by dividing a square of side length $ n $ into unit squares using lines parallel to the sides of the square, we consider all squares whose sides are contained in the lines forming the chessboard. Let $ 1 \leq k \leq n $ and $ P(k,n) $ denote the number of these squares whose side lengths do not exceed $ k $. Let $ k(n) $ be the largest of such numbers $ k $ for which $ P(k, n) \leq \frac{1}{2} P(n, n) $. Calculate $ \lim_{n\to \infty} \frac{k(n)}{n} $.
|
{"ground_truth": "\\frac{\\sqrt[3]{4}}{2}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 314
|
numina_1.5_356
|
verifiable_math
|
XXXIX OM - III - Problem 6
Calculate the maximum volume of a tetrahedron contained within a hemisphere of radius 1.
|
{"ground_truth": "\\frac{\\sqrt{3}}{4}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 315
|
numina_1.5_359
|
verifiable_math
|
XLV OM - II - Task 4
Each vertex of a cube is assigned the number $ 1 $ or $ -1 $, and each face is assigned the product of the numbers assigned to the vertices of that face. Determine the set of values that the sum of the $ 14 $ numbers assigned to the faces and vertices can take.
|
{"ground_truth": "{14,10,6,2,-2,-6,-10,-14}\\setminus{10,-14}={14,6,2,-2,-6,-10}"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 316
|
numina_1.5_360
|
verifiable_math
|
XLVI OM - I - Zadanie 1
Wyznaczyć wszystkie pary $ (x,y) $ liczb naturalnych, dla których liczby $ \frac{x+1}{y} $ oraz $ \frac{y+1}{x} $ są naturalne.
|
{"ground_truth": "(3,2),(2,3),(1,1),(2,1),(1,2)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 317
|
numina_1.5_361
|
verifiable_math
|
XVIII OM - I - Zadanie 10
Trójka liczb całkowitych tworzy postęp geometryczny o ilorazie całkowitym. Gdy najmniejszą z nich zwiększymy o 9, powstanie postęp arytmetyczny. Jakie to liczby?
|
{"ground_truth": "(-1,-4,-16),(-1,2,-4),(-9,-18,-36),(2,-4,8)"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 318
|
numina_1.5_362
|
verifiable_math
|
LV OM - II - Task 4
Determine all positive integers $ n $ that have exactly $ \sqrt{n} $ positive divisors.
|
{"ground_truth": "n=1n=9"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 319
|
numina_1.5_363
|
verifiable_math
|
XXVII OM - I - Zadanie 4
Samolot leci bez zatrzymywania się po najkrótszej drodze z Oslo do miasta $ X $ leżącego na równiku w Ameryce Południowej. Z Oslo startuje dokładnie w kierunku zachodnim. Wiedząc, że współrzędne geograficzne Oslo są : $ 59^{\circ}55 szerokości północnej i $ 10^{\circ}43 długości wschodniej, obliczyć współrzędne geograficzne miasta $ X $. Jakie to miasto? Obliczyć długość drogi samolotu z dokładnością do 100 km. Zakładamy, że Ziemia jest idealną kulą o długości równika 40 000 km oraz, że samolot leci na wysokości nie większej niż 10 km.
|
{"ground_truth": "Quito,10000"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 320
|
numina_1.5_366
|
verifiable_math
|
XLIII OM - I - Problem 2
In square $ABCD$ with side length $1$, point $E$ lies on side $BC$, point $F$ lies on side $CD$, the measures of angles $EAB$ and $EAF$ are $20^{\circ}$ and $45^{\circ}$, respectively. Calculate the height of triangle $AEF$ drawn from vertex $A$.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 321
|
numina_1.5_367
|
verifiable_math
|
I OM - B - Task 3
Someone has an unbalanced two-pan scale (i.e., a scale
whose arms are unequal). Wanting to weigh 2 kg of sugar, they proceed
as follows: they place a 1 kg weight on the left pan of the scale,
and pour sugar onto the right pan until it balances; then:
after emptying both pans, they place the 1 kg weight on the right pan, and pour sugar onto the left pan until it balances. Do the two
amounts of sugar weighed in this way together weigh less, or more, or exactly
2 kg?
|
{"ground_truth": "More\\than\\2\\"}
|
{"source": "olympiads", "problem_type": "Logic and Puzzles"}
| 322
|
numina_1.5_370
|
verifiable_math
|
XIX OM - III - Problem 1
What is the largest number of regions into which a plane can be divided by $ n $ pairs of parallel lines?
|
{"ground_truth": "2n^2-n+1"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 323
|
numina_1.5_372
|
verifiable_math
|
XLV OM - II - Task 1
Determine all polynomials $ P(x) $ of degree at most fifth with real coefficients, having the property that the polynomial $ P(x) + 1 $ is divisible by $ (x - 1)^3 $ and the polynomial $ P(x) - 1 $ is divisible by $ (x + 1)^3 $.
|
{"ground_truth": "P(x)=-\\frac{1}{8}x^5+\\frac{5}{8}x^3-\\frac{15}{8}x"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 324
|
numina_1.5_373
|
verifiable_math
|
XVIII OM - I - Problem 5
Find such natural numbers $ p $ and $ q $, so that the roots of the equations $ x^2 - qx + p = 0 $ and $ x^2 - px + q = 0 $ are natural numbers.
|
{"ground_truth": "p=4,\\p="}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 325
|
numina_1.5_374
|
verifiable_math
|
LIX OM - I - Task 12
Given an integer $ m \geqslant 2 $. Determine the smallest such integer
$ n \geqslant m $, such that for any partition of the set $ \{m,m+1,\dots ,n\} $ into two subsets, at least one of
these subsets contains numbers $ a, b, c $ (not necessarily distinct), such that $ ab = c $.
|
{"ground_truth": "^5"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 326
|
numina_1.5_375
|
verifiable_math
|
XV OM - I - Problem 10
Find the $ n $-th term of the sequence of numbers $ a_1, a_2, a_n, \ldots $, where $ a_1 = 1 $, $ a_2 = 3 $, $ a_3 = 6 $, and for every natural number $ k $
|
{"ground_truth": "\\frac{n(n+1)}{2}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 327
|
numina_1.5_376
|
verifiable_math
|
XLVI OM - III - Problem 1
Determine the number of subsets of the set $ \{1,2, \ldots , 2n\} $ in which the equation $ x + y = 2n+1 $ has no solutions.
|
{"ground_truth": "3^n"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 328
|
numina_1.5_377
|
verifiable_math
|
XLVIII OM - I - Problem 8
Let $ a_n $ be the number of all non-empty subsets of the set $ \{1,2,\ldots,6n\} $, the sum of whose elements gives a remainder of 5 when divided by 6, and let $ b_n $ be the number of all non-empty subsets of the set $ \{1,2,\ldots,7n\} $, the product of whose elements gives a remainder of 5 when divided by 7. Calculate the quotient $ a_n/b_n $.
|
{"ground_truth": "1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 329
|
numina_1.5_378
|
verifiable_math
|
XLIX OM - I - Problem 4
Given a positive number $ a $. Determine all real numbers $ c $ that have the following property: for every pair of positive numbers $ x $, $ y $, the inequality $ (c-1)x^{a+1} \leq (cy - x)y^a $ is satisfied.
|
{"ground_truth": "\\frac{}{+1}"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 330
|
numina_1.5_379
|
verifiable_math
|
L OM - I - Problem 11
In an urn, there are two balls: a white one and a black one. Additionally, we have 50 white balls and 50 black balls at our disposal. We perform the following action 50 times: we draw a ball from the urn, and then return it to the urn along with one more ball of the same color as the drawn ball. After completing these actions, we have 52 balls in the urn. What is the most probable number of white balls in the urn?
|
{"ground_truth": "51"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 331
|
numina_1.5_382
|
verifiable_math
|
XLVI OM - III - Problem 2
The diagonals of a convex pentagon divide this pentagon into a pentagon and ten triangles. What is the maximum possible number of triangles with equal areas?
|
{"ground_truth": "6"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 332
|
numina_1.5_383
|
verifiable_math
|
XXVII OM - III - Task 5
A fishing vessel is fishing in the territorial waters of a foreign state without permission. Each cast of the net results in a catch of the same value. During each subsequent cast, the probability of the vessel being intercepted by the border guard is $ \frac{1}{k} $, where $ k $ is a fixed natural number. We assume that the event of the vessel being intercepted or not intercepted during each subsequent cast is independent of the previous course of the fishing. If intercepted by the border guard, the entire catch is confiscated, and further fishing is impossible. The captain plans to return after the $ n $-th cast. Considering the risk of interception, the profit from fishing is a random variable. Find the number $ n $ for which the expected value of the profit is maximized.
|
{"ground_truth": "n=k-1n=k"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 333
|
numina_1.5_384
|
verifiable_math
|
XXII OM - I - Problem 4
Determine the angles that a plane passing through the midpoints of three skew edges of a cube makes with the faces of the cube.
|
{"ground_truth": "5445"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 334
|
numina_1.5_385
|
verifiable_math
|
XXXVI OM - I - Problem 6
Calculate the lengths of the parallel sides of a trapezoid given the lengths of the other sides and the diagonals.
|
{"ground_truth": "\\frac{2(p^2-q^2)}{b^2-^2+p^2-q^2},\\quad\\frac{2(q^2-p^2)}{b^2-^2+q^2-p^2}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 335
|
numina_1.5_386
|
verifiable_math
|
XXXVI OM - II - Problem 3
Let $ L $ be the set of all broken lines $ ABCDA $, where $ A, B, C, D $ are distinct vertices of a fixed regular 1985-gon. A broken line is randomly chosen from the set $ L $. Calculate the probability that it is the boundary of a convex quadrilateral.
|
{"ground_truth": "\\frac{1}{3}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 336
|
numina_1.5_387
|
verifiable_math
|
XXVIII - II - Task 6
What is the maximum number of parts that the edges of $ n $ squares can divide a plane into?
|
{"ground_truth": "(2n-1)^2+1"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 337
|
numina_1.5_388
|
verifiable_math
|
LIX OM - I - Task 9
Determine the smallest real number a with the following property:
For any real numbers $ x, y, z \geqslant a $ satisfying the condition $ x + y + z = 3 $
the inequality holds
|
{"ground_truth": "-5"}
|
{"source": "olympiads", "problem_type": "Inequalities"}
| 338
|
numina_1.5_389
|
verifiable_math
|
XLIV OM - I - Problem 11
In six different cells of an $ n \times n $ table, we place a cross; all arrangements of crosses are equally probable. Let $ p_n $ be the probability that in some row or column there will be at least two crosses. Calculate the limit of the sequence $ (np_n) $ as $ n \to \infty $.
|
{"ground_truth": "30"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 339
|
numina_1.5_393
|
verifiable_math
|
XV OM - I - Problem 7
Given a circle and points $ A $ and $ B $ inside it. Find a point $ P $ on this circle such that the angle $ APB $ is subtended by a chord $ MN $ equal to $ AB $. Does the problem have a solution if the given points, or only one of them, lie outside the circle?
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 340
|
numina_1.5_394
|
verifiable_math
|
VI OM - III - Task 6
Through points $ A $ and $ B $, two oblique lines $ m $ and $ n $ perpendicular to the line $ AB $ have been drawn. On line $ m $, a point $ C $ (different from $ A $) has been chosen, and on line $ n $, a point $ D $ (different from $ B $). Given the lengths of segments $ AB = d $ and $ CD = l $, and the angle $ \varphi $ formed by the oblique lines $ m $ and $ n $, calculate the radius of the sphere passing through points $ A $, $ B $, $ C $, $ D $.
|
{"ground_truth": "\\sqrt{(\\frac{}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 341
|
numina_1.5_395
|
verifiable_math
|
XLVI OM - I - Problem 6
Inside triangle $ABC$, a point $P$ is chosen. Lines $AP$, $BP$, $CP$ intersect sides $BC$, $CA$, $AB$ at points $A'$, $B'$, $C'$ respectively. Let: $u = |AP|:|PA'|$, $v = |BP|:|PB'|$, $w = |CP|:|PC'$. Express the product $uvw$ in terms of the sum $u + v + w$.
|
{"ground_truth": "uvw=u+v+w+1"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 342
|
numina_1.5_396
|
verifiable_math
|
I OM - B - Task 20
The sides of a right-angled triangle are expressed by natural numbers. One of the legs is expressed by the number 10. Calculate the remaining sides of this triangle.
|
{"ground_truth": "x=26,y=24"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 343
|
numina_1.5_397
|
verifiable_math
|
I OM - B - Task 4
Find two natural numbers $ a $ and $ b $ given their greatest common divisor
$ D=12 $ and least common multiple $ M=432 $. Provide a method for finding
solutions in the general case.
|
{"ground_truth": "(12,"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 344
|
numina_1.5_398
|
verifiable_math
|
XLV OM - III - Task 1
Determine all triples $ (x,y,z) $ of positive rational numbers for which the numbers $ x+y+z $, $ \frac{1}{x}+\frac{1}{y}+\frac{1}{z} $, $ xyz $ are natural.
|
{"ground_truth": "(1,1,1),(2,2,1),(2,1,2),(1,2,2)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 345
|
numina_1.5_399
|
verifiable_math
|
XXVI - I - Task 1
At the ball, there were 42 people. Lady $ A_1 $ danced with 7 gentlemen, Lady $ A_2 $ danced with 8 gentlemen, ..., Lady $ A_n $ danced with all the gentlemen. How many gentlemen were at the ball?
|
{"ground_truth": "24"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 346
|
numina_1.5_400
|
verifiable_math
|
I OM - B - Task 5
A motorboat set off upstream at 9:00, and at the same moment, a ball was thrown from the motorboat into the river. At 9:15, the motorboat turned around and started moving downstream. At what time did the motorboat catch up with the ball?
|
{"ground_truth": "9:30"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 347
|
numina_1.5_401
|
verifiable_math
|
XXXV OM - III - Task 4
We toss a coin $ n $ times and record the result as a sequence $ (a_1, a_2, \ldots, a_n) $, where $ a_i = 1 $ or $ a_i = 2 $ depending on whether an eagle or a tail appeared in the $ i $-th toss. We assume $ b_j = a_1 + a_2 + \ldots + a_j $ for $ j = 1, 2, \ldots, n $, $ p(n) $ is the probability that the number $ n $ appears in the sequence $ (b_1, b_2, \ldots, b_n) $. Determine $ p(n) $ in terms of $ p(n-1) $ and $ p(n-2) $.
|
{"ground_truth": "p(n)=\\frac{1}{2}p(n-1)+\\frac{1}{2}p(n-2)"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 348
|
numina_1.5_402
|
verifiable_math
|
XLIX OM - I - Zadanie 2
Proste zawierające wysokości trójkąta $ ABC $, wpisanego w okrąg o środku $ O $, przecinają się w punkcie $ H $, przy czym $ |AO| =|AH| $. Obliczyć miarę kąta $ CAB $.
|
{"ground_truth": "60or120"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 349
|
numina_1.5_403
|
verifiable_math
|
L OM - II - Task 5
Let $ S = \{1, 2,3,4, 5\} $. Determine the number of functions $ f: S \to S $ satisfying the equation $ f^{50} (x) = x $ for all $ x \in S $.
Note: $ f^{50}(x) = \underbrace{f \circ f \circ \ldots \circ f}_{50} (x) $.
|
{"ground_truth": "50"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 350
|
numina_1.5_404
|
verifiable_math
|
XXXIII OM - I - Problem 1
A regular 25-gon $ A_1, A_2, \ldots, A_{25} $ is inscribed in a circle with center $ O $ and radius of length $ r $. What is the maximum length of the vector that is the sum of some of the vectors $ \overrightarrow{OA_1}, \overrightarrow{OA_2}, \ldots, \overrightarrow{OA_{25}} $?
|
{"ground_truth": "2r\\cos\\frac{6\\pi}{25}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 351
|
numina_1.5_405
|
verifiable_math
|
XIII OM - III - Task 3
What condition should the angles of triangle $ ABC $ satisfy so that the angle bisector of $ A $, the median drawn from vertex $ B $, and the altitude drawn from vertex $ C $ intersect at one point?
|
{"ground_truth": "\\tanA\\cdot\\cosB=\\sinC"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 352
|
numina_1.5_407
|
verifiable_math
|
LIII OM - III - Task 1
Determine all such triples of natural numbers $ a $, $ b $, $ c $, such that the numbers $ a^2 +1 $ and $ b^2 +1 $ are prime and
|
{"ground_truth": "(1,2,3)(2,1,3)"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 353
|
numina_1.5_408
|
verifiable_math
|
XII OM - III - Task 6
Someone wrote six letters to six people and addressed six envelopes to them. In how many ways can the letters be placed into the envelopes so that no letter ends up in the correct envelope?
|
{"ground_truth": "265"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 354
|
numina_1.5_409
|
verifiable_math
|
II OM - I - Task 10
A circle is circumscribed around triangle $ ABC $. Given the radius $ R $ of this circle, calculate the radius of the circle passing through the centers of the three excircles (inscribed in the angles) of triangle $ ABC $.
|
{"ground_truth": "2R"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 355
|
numina_1.5_410
|
verifiable_math
|
IV OM - III - Task 5
A car departs from point $ O $ and drives along a straight road at a constant speed $ v $. A cyclist, who is at a distance $ a $ from point $ O $ and at a distance $ b $ from the road, wishes to deliver a letter to the car. What is the minimum speed at which the cyclist should ride to achieve his goal?
|
{"ground_truth": "v\\sin\\alpha"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 356
|
numina_1.5_411
|
verifiable_math
|
XXIII OM - I - Problem 9
How many natural numbers less than $ 10^n $ have a decimal representation whose digits form a non-decreasing sequence?
|
{"ground_truth": "\\binom{n+9}{9}-1"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 357
|
numina_1.5_412
|
verifiable_math
|
XLIII OM - II - Problem 5
Determine the supremum of the volumes of spheres contained in tetrahedra with all altitudes no longer than $1$.
|
{"ground_truth": "\\pi/48"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 358
|
numina_1.5_414
|
verifiable_math
|
LI OM - III - Task 5
For a given natural number $ n \geq 2 $, find the smallest number $ k $ with the following property. From any $ k $-element set of fields of the $ n \times n $ chessboard, one can select a non-empty subset such that the number of fields of this subset in each row and each column of the chessboard is even.
|
{"ground_truth": "2n"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 359
|
numina_1.5_415
|
verifiable_math
|
XXII OM - III - Task 3
How many locks at least need to be placed on the treasury so that with a certain distribution of keys among the 11-member committee authorized to open the treasury, any 6 members can open it, but no 5 can? Determine the distribution of keys among the committee members with the minimum number of locks.
|
{"ground_truth": "462"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 360
|
numina_1.5_416
|
verifiable_math
|
LVIII OM - I - Problem 4
For each natural number $ n\ge 3 $, determine the number of sequences $ (c_1,c_2,\ldots,c_n) $, where $ {c_i\in\{0,1,\ldots,9\}} $, with the following property:\break in every triple of consecutive terms, there are at least two terms that are equal.
|
{"ground_truth": "5\\cdot(4^n+(-2)^n)"}
|
{"source": "olympiads", "problem_type": "Combinatorics"}
| 361
|
numina_1.5_418
|
verifiable_math
|
1. Let $\log _{2} x=m \in Z, m>0, \log _{6} y=n \in Z, n>0$.
Then $x=2^{m}, y=6^{n}$. As a result, we have
$$
\text { GCD }(x, y)=\text { GCD }\left(2^{m}, 6^{n}\right)=\text { GCD }\left(2^{m}, 2^{n} \cdot 3^{n}\right)=8=2^{3} .
$$
Case 1. $m \geq n$. Then $n=3, \quad y=6^{3}=216$,
GCD $\left(\log _{2} x, 3\right)=3$. From this, we find $\log x=B k=$ or $x=8^{k}, k \in Z$.
Case 2. $m0$ or $y=216^{s}, s \in Z, s>0$.
|
{"ground_truth": "8^{k},k=1,2,\\ldots;216\\text"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 362
|
numina_1.5_419
|
verifiable_math
|
3. Since the right side of the equation $(x+y)^{2}=49(3 x+5 y)$ is divisible by 49, then $x+y=7 k$. Substituting this into the equation, we get $49 k^{2}=49(3 x+5 y)$ or $3 x+5 y=k^{2}$. Solving the system
$$
\left\{\begin{array}{c}
3 x+5 y=k^{2} \\
x+y=7 k
\end{array}\right.
$$
we find
$$
\left\{\begin{array}{l}
x=\frac{k(35-k)}{2} \\
y=\frac{k(k-21)}{2}
\end{array} k \in Z\right.
$$
From the obtained solutions, we need to select those for which $x$ and $y$ are integers. Since the numbers $k$ and $35-k$ and $k$ and $k-21$ have different parities, the numerators of both fractions are even for any integer $k$, and therefore, the fractions themselves are integers.
|
{"ground_truth": "{\\begin{pmatrix}\\frac{k(35-k)}{2},\\\\\\frac{k(k-21)}{2},\\end{pmatrix}k\\inZ.}"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 363
|
numina_1.5_420
|
verifiable_math
|
4. Each experience of throwing the circle corresponds to a point $M-$ the position of the center of the circle on the vertical segment $[A ; B]$ of length 1.
Let's introduce the following notations: $R$ - the radius of the circle, $O$ - the midpoint of the segment $[A ; B], \quad O M=x \in[0 ; 0.5]$ - a random variable uniformly distributed on this segment, $\alpha$ - the angle indicated in the figure, $A M=h=\frac{\cos \alpha}{2}$.
The area of the circular segment $S_{1}$ of a circle with radius $R$ is given by the formula:
$$
S_{1}=\left|\alpha R^{2}-\frac{1}{2} R^{2} \sin 2 \alpha\right|
$$
In our case, $R=\frac{1}{2}$, so,
$$
S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8} .
$$
From the problem statement, it follows that
$$
\left\{\begin{array}{c}
S_{1}: S_{2}=(\pi-2):(3 \pi+2) \\
S_{1}+S_{2}=\frac{\pi}{4}
\end{array}\right.
$$
Then $S_{1}=k(\pi-2)$, and $S_{2}=k(3 \pi+2)$. Substituting this into the second equality, we get: $S_{1}+S_{2}=k \cdot 4 \pi=\frac{\pi}{4}$. Therefore, $k=\frac{1}{16}$. Then, $S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8}=\frac{1}{16}(\pi-2)$. From this, we find $\alpha=\frac{\pi}{4}$. Thus, the conditions of the problem correspond to the central angle $P M Q$ equal to $\frac{\pi}{2}$. Then $h=\frac{\sqrt{2}}{4}$ and the favorable outcome of the experiment corresponds to points $M$ that are no more than $\frac{1}{2}-h=\frac{2-\sqrt{2}}{4}$ away from point $O$. Since the probability of the desired event is the ratio of the length of the segment of "favorable" outcomes, i.e., $\frac{2-\sqrt{2}}{2}$ to the length of the segment $[A ; B]$, i.e., to one, the desired probability $P(A)=\frac{2-\sqrt{2}}{2} \approx 0.29$
|
{"ground_truth": "P(A)=\\frac{2-\\sqrt{2}}{2}\\approx0.29"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 364
|
numina_1.5_421
|
verifiable_math
|
6. Let's introduce the following notations: $S$ - the area of the trapezoid, $S_{1}$ - the area of triangle $ABC$, $S_{2}$ - the area of triangle $ACD$, $h$ - the height of the trapezoid, $\gamma=\frac{q}{p}$, $\mu=\frac{n}{m}$.
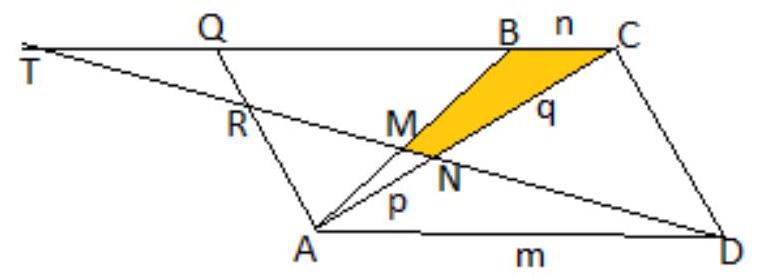
We have $S_{1}: S_{2}=\frac{n}{m}$ because these triangles have the same height. Therefore, $S_{1}=\frac{n}{n+m} \cdot S$. From the similarity of triangles $AND$ and $CNT$, it follows that $\frac{TC}{AD}=\frac{q}{p}$. From this equality, we get: $TC=\frac{q}{p} AD$. Then $TB=TC-BC=\frac{q}{p} AD-\frac{n}{m} AD=\left(\frac{q}{p}-\frac{n}{m}\right) AD$. From the similarity of triangles $AMD$ and $BTM$, it follows that
$$
\mathrm{BM}: \mathrm{AM}=TB: AD=\left(\frac{q}{p}-\frac{n}{m}\right)
$$
Therefore,
$$
\frac{AM}{AB}=\frac{AM}{AM+MB}=\frac{1}{1+BM: AM}=\frac{1}{1+\frac{q}{p}-\frac{n}{m}}
$$
Then
$$
S_{AMN}=\frac{AM}{AB} \cdot \frac{p}{p+q} \cdot S_{1}=\frac{1}{1+\frac{q}{p}-\frac{n}{m}} \cdot \frac{1}{1+\frac{q}{p}} \cdot S_{1}=\frac{1}{1+\gamma-\mu} \cdot \frac{1}{1+\gamma} \cdot S_{1}
$$
From this, we get
$$
\begin{gathered}
S_{MBCN}=S_{1}-S_{AMN}=\left(1-\frac{1}{1+\gamma-\mu} \cdot \frac{1}{1+\gamma}\right) S_{1}= \\
=\left(1-\frac{1}{1+\gamma-\mu} \cdot \frac{1}{1+\gamma}\right) \frac{\mu}{1+\mu} S
\end{gathered}
$$
In our problem, $\gamma=2, \mu=\frac{1}{3}$, so $S_{MBCN}: S=7: 32$.
|
{"ground_truth": "S_{MBCN}:S=7:32"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 365
|
numina_1.5_422
|
verifiable_math
|
1. Natural numbers $x$ and $y$ are such that their $\operatorname{GCD}(x, y)=16$, and $\operatorname{LCM}\left(\log _{8} x, \log _{12} y\right)=18$. Find these numbers.
|
{"ground_truth": "8^{9},144;8^{18},144"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 366
|
numina_1.5_423
|
verifiable_math
|
3. Find all pairs of integers $(x ; y)$ that satisfy the equation $(x-y)^{2}=25(2 x-3 y)$.
|
{"ground_truth": "(15-),(10-),\\inZ"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 367
|
numina_1.5_424
|
verifiable_math
|
4. On a plane, an infinite number of parallel lines are drawn, each separated from the next by a distance of 1. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts such that the ratio of the areas (of the smaller to the larger part) does not exceed the number \((4 \pi - 3 \sqrt{3}) : (8 \pi + 3 \sqrt{3})\).
|
{"ground_truth": "\\frac{1}{2}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 368
|
numina_1.5_425
|
verifiable_math
|
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x+2+2 \sqrt{2} \cos a)^{2}+(y-1-2 \sqrt{2} \sin a)^{2}=2 \\ (x-y+3)(x+y+1)=0\end{array}\right.$ have three
solutions?
|
{"ground_truth": "a_{1}=\\frac{7\\pi}{12}+\\pik,a_{2}=\\frac{11\\pi}{12}+\\pik,k\\inZ"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 369
|
numina_1.5_426
|
verifiable_math
|
6. Point $N$ divides the diagonal $A C$ of trapezoid $A B C D$ in the ratio $C N: N A=3$. The lengths of the bases $B C$ and $A D$ of the trapezoid are in the ratio $1: 2$. A line is drawn through point $N$ and vertex $D$, intersecting the lateral side $A B$ at point $M$. What fraction of the area of the trapezoid is the area of quadrilateral $M B C N$?
|
{"ground_truth": "13:42"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 370
|
numina_1.5_427
|
verifiable_math
|
1. Natural numbers $x$ and $y$ are such that their LCM $(x, y)=3^{6} \cdot 2^{8}$, and GCD $\left(\log _{3} x, \log _{12} y\right)=2$. Find these numbers.
|
{"ground_truth": "3^{6}=729,12^{4}=20736"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 371
|
numina_1.5_428
|
verifiable_math
|
3. Find all pairs of integers $(x ; y)$ that satisfy the equation $(x+2 y)^{2}=9(x+y)$.
|
{"ground_truth": "(2-3),(3-),\\inZ"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 372
|
numina_1.5_429
|
verifiable_math
|
4. On a plane, an infinite number of parallel lines are drawn, each separated from the next by a distance of 1. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts such that the ratio of the areas (of the smaller to the larger part) does not exceed the number \((2 \pi - 3 \sqrt{3}) : (10 \pi + 3 \sqrt{3})\).
|
{"ground_truth": "\\frac{2-\\sqrt{3}}{2}"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 373
|
numina_1.5_430
|
verifiable_math
|
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x-2-\sqrt{5} \cos a)^{2}+(y+1-\sqrt{5} \sin a)^{2}=\frac{5}{4} \text { have two solutions? } \\ (x-2)(x-y-3)=0\end{array}\right.$
|
{"ground_truth": "\\in(\\frac{\\pi}{12}+\\pik;\\frac{\\pi}{3}+\\pik)\\cup(\\frac{5\\pi}{12}+\\pik;\\frac{2\\pi}{3}+\\pik),k\\inZ"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 374
|
numina_1.5_431
|
verifiable_math
|
6. Point $N$ divides the diagonal $A C$ of trapezoid $A B C D$ in the ratio $C N: N A=4$. The lengths of the bases $B C$ and $A D$ of the trapezoid are in the ratio $2: 3$. A line is drawn through point $N$ and vertex $D$, intersecting the lateral side $A B$ at point $M$. What fraction of the area of the trapezoid is the area of quadrilateral $M B C N$?
|
{"ground_truth": "124:325"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 375
|
numina_1.5_432
|
verifiable_math
|
1. Natural numbers $x$ and $y$ are such that their LCM $(x, y)=5^{4} \cdot 2^{6}$, and LCM $\left(\log _{10} x, \log _{40} y\right)=4$. Find these numbers.
|
{"ground_truth": "10^{4},40^{2}"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 376
|
numina_1.5_434
|
verifiable_math
|
4. On a plane, an infinite number of parallel lines are drawn, each at a distance of 1 from each other. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts, the ratio of the areas of which (the smaller to the larger) does not exceed the number \((5 \pi - 3):(7 \pi + 3)\)
|
{"ground_truth": "P(A)=\\frac{2-\\sqrt{2-\\sqrt{3}}}{2}\\approx0.74"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 377
|
numina_1.5_435
|
verifiable_math
|
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x-2-3 \cos a)^{2}+(y+2-3 \sin a)^{2}=1 \\ (y+2)(x+y)=0\end{array}\right.$ have a unique solution?
|
{"ground_truth": "a_{1}=\\\\arcsin\\frac{1}{3}+\\pik,a_{2}=-\\frac{\\pi}{4}\\\\arcsin\\frac{1}{3}+\\pik,k\\inZ"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 378
|
numina_1.5_436
|
verifiable_math
|
6. Point $N$ divides the diagonal $A C$ of trapezoid $A B C D$ in half. The lengths of the bases $B C$ and $A D$ of the trapezoid are in the ratio $1: 4$. A line is drawn through point $N$ and vertex $D$, intersecting the lateral side $A B$ at point $M$. What fraction of the area of the trapezoid is the area of quadrilateral $M B C N$?
|
{"ground_truth": "1:7"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 379
|
numina_1.5_437
|
verifiable_math
|
1. Let $m$ be the number of coins in the treasure. Then the number of remaining coins $N$ in the morning is
$$
\begin{gathered}
N=\frac{2}{3}\left(\frac{2}{3}\left(\frac{2}{3}(m-1)-1\right)-1\right)=\frac{2^{3}}{3^{3}}(m-1)-\frac{2}{3}-\frac{2^{2}}{3^{2}} \\
N=\frac{2^{3}}{3^{3}}(m-1)-\frac{10}{9}=3 n \\
8(m-1)-30=81 k, \text { then }\left\{\begin{array}{c}
m-1=3 t, \\
8 t-27 k=10
\end{array},\left\{\begin{array}{c}
m=3 t+1 \\
k=2 s \\
4 t-27 s=5
\end{array}\right.\right. \\
\left\{\begin{array}{c}
m=3 t+1 \\
k=2 s, \\
t=8+27 u, \\
s=1+4 u
\end{array}\right.
\end{gathered}
$$
Considering the constraints
$$
\begin{gathered}
110 \leq 81 u+25 \leq 200, \text { so } u=2, m=187 . \\
m_{1}=1+\frac{187-1}{3}=63, \quad \widetilde{m}_{1}=63+18=81 \\
- \text { the money of the first pirate; } \\
m_{2}=1+\frac{187-63-1}{3}=42, \quad \widetilde{m}_{2}=42+18=60 \\
m_{3}=1+\frac{187-63-42-1}{3}=28, \quad \widetilde{m}_{3}=28+18=46 \\
- \text { the money of the third pirate; } \\
m_{0}=\frac{187-63-42-28}{3}=18 \\
\text {- the money each received in the morning. }
\end{gathered}
$$
|
{"ground_truth": "81,60,46"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 380
|
numina_1.5_438
|
verifiable_math
|
3. For which natural numbers $n$ can the fraction $\frac{3}{n}$ be represented as a periodic decimal fraction of the form $0.1\left(a_{1} a_{2}\right)$ with a period containing two different digits?
|
{"ground_truth": "n=22;a_{1}=3,a_{2}=6"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 381
|
numina_1.5_439
|
verifiable_math
|
4. Consider the set $M$ of integers $n \in[-100 ; 500]$, for which the expression $A=n^{3}+2 n^{2}-5 n-6$ is divisible by 11. How many integers are contained in $M$? Find the largest and smallest of them?
|
{"ground_truth": "164"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 382
|
numina_1.5_441
|
verifiable_math
|
3. For which natural numbers $n$ can the fraction $\frac{4}{n}$ be represented as a periodic decimal fraction of the form $0.1\left(a_{1} a_{2} a_{3}\right)$ with a period containing at least two different digits?
|
{"ground_truth": "n=27;a_{1}=4,a_{2}=8,a_{3}=1n=37;a_{1}=0,a_{2}=8,a_{3}=2"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 383
|
numina_1.5_442
|
verifiable_math
|
4. Consider the set $M$ of integers $n \in[-30 ; 100]$, for which the expression $A=n^{3}+4 n^{2}+n-6$ is divisible by 5. How many integers are contained in $M$? Find the largest and smallest of them.
|
{"ground_truth": "78,n_{\\}=-29,n_{\\max}=98"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 384
|
numina_1.5_443
|
verifiable_math
|
1. A crew of four pirates docked at an island to divide a treasure of gold coins left there. It was late, so they decided to postpone the division until morning. The first pirate woke up in the middle of the night and decided to take his share. He couldn't divide the coins into four equal parts, so he took two coins first, and then a quarter of the remaining coins, and went back to sleep. Unaware of this, the second pirate woke up during the night and did the same as the first. The third and fourth pirates repeated what the first and second had done. In the morning, without saying a word to each other, they divided the remaining coins equally among themselves. How many coins did each pirate get if the original treasure contained no fewer than 3000 and no more than 4000 coins?
|
{"ground_truth": "1178"}
|
{"source": "olympiads", "problem_type": "Logic and Puzzles"}
| 385
|
numina_1.5_444
|
verifiable_math
|
3. For which natural numbers $n$ can the fraction $\frac{5}{n}$ be represented as a periodic decimal fraction of the form $0.1\left(a_{1} a_{2} a_{3}\right)$ with a period containing at least two different digits?
|
{"ground_truth": "n=27;a_{1}=8,a_{2}=5,a_{3}=1orn=37;a_{1}=3,a_{2}=5,a_{3}=1"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 386
|
numina_1.5_445
|
verifiable_math
|
4. Consider the set $M$ of integers $n \in[-50 ; 250]$, for which the expression $A=n^{3}-2 n^{2}-13 n-10$ is divisible by 13. How many integers are contained in $M$? Find the largest and smallest of them?
|
{"ground_truth": "69,n_{\\}=-47,n_{\\max}=246"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 387
|
numina_1.5_446
|
verifiable_math
|
1. Solution. According to the problem, the sum of the original numbers is represented by the expression:
$$
\begin{aligned}
& \left(a_{1}+2\right)^{2}+\left(a_{2}+2\right)^{2}+\ldots+\left(a_{50}+2\right)^{2}=a_{1}^{2}+a_{2}^{2}+\ldots+a_{50}^{2} \rightarrow \\
& {\left[\left(a_{1}+2\right)^{2}-a_{1}^{2}\right]+\left[\left(a_{2}+2\right)^{2}-a_{2}^{2}\right]+\ldots\left[\left(a_{50}+2\right)^{2}-a_{50}^{2}\right]=0 \rightarrow} \\
& \rightarrow 4\left(a_{1}+1\right)+4\left(a_{2}+1\right)+\ldots+4\left(a_{50}+1\right)=0 \rightarrow a_{1}+a_{2}+\ldots+a_{50}=-50
\end{aligned}
$$
Then, if we add 3, we get:
$$
\begin{aligned}
& \left(a_{1}+3\right)^{2}+\left(a_{2}+3\right)^{2}+\ldots+\left(a_{50}+3\right)^{2}-\left(a_{1}^{2}+a_{2}^{2}+\ldots+a_{50}^{2}\right)= \\
& =\left[\left(a_{1}+3\right)^{2}-a_{1}^{2}\right]+\left[\left(a_{2}+3\right)^{2}-a_{2}^{2}\right]+\ldots\left[\left(a_{50}+3\right)^{2}-a_{50}^{2}\right]= \\
& =3\left(2 a_{1}+3\right)+3\left(2 a_{2}+3\right)+\ldots+3\left(2 a_{50}+3\right)=6\left(a_{1}+a_{2}+\ldots+a_{50}\right)+9 \cdot 50= \\
& =-300+450=150
\end{aligned}
$$
|
{"ground_truth": "150"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 388
|
numina_1.5_447
|
verifiable_math
|
1. A set of 60 numbers is such that adding 3 to each of them does not change the value of the sum of their squares. By how much will the sum of the squares of these numbers change if 4 is added to each number?
|
{"ground_truth": "240"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 389
|
numina_1.5_448
|
verifiable_math
|
5. The length of the diagonal $AC$ of the rhombus $ABCD$ with an acute angle at vertex $A$ is 4. Points $M$ and $N$ on sides $DA$ and $DC$ are the feet of the altitudes of the rhombus dropped from vertex $B$.
The height $BM$ intersects the diagonal $AC$ at point $P$ such that $AP: PC=1: 4$. Find the length of the segment $MN$.
|
{"ground_truth": "3"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 390
|
numina_1.5_449
|
verifiable_math
|
1. A set of 70 numbers is such that adding 4 to each of them does not change the magnitude of the sum of their squares. By how much will the sum of the squares of these numbers change if 5 is added to each number?
|
{"ground_truth": "350"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 391
|
numina_1.5_450
|
verifiable_math
|
5. The length of the diagonal $AC$ of the rhombus $ABCD$ with an acute angle at vertex $A$ is 12. Points $M$ and $N$ on sides $DA$ and $DC$ are the bases of the heights of the rhombus dropped from vertex $B$. The height $BM$ intersects the diagonal $AC$ at point $P$ such that $AP: PC = 2: 3$. Find the length of the segment $MN$.
|
{"ground_truth": "4"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 392
|
numina_1.5_451
|
verifiable_math
|
1. A set of 80 numbers is such that adding 5 to each of them does not change the magnitude of the sum of their squares. By how much will the sum of the squares of these numbers change if 6 is added to each number?
|
{"ground_truth": "480"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 393
|
numina_1.5_452
|
verifiable_math
|
5. The length of the diagonal $AC$ of the rhombus $ABCD$ with an acute angle at vertex $A$ is 20. Points $M$ and $N$ on sides $DA$ and $DC$ are the bases of the heights of the rhombus dropped from vertex $B$. The height $BM$ intersects the diagonal $AC$ at point $P$ such that $AP: PC=3: 4$. Find the length of the segment $MN$.
|
{"ground_truth": "5"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 394
|
numina_1.5_453
|
verifiable_math
|
1. Find the largest solution on the interval $[0 ; 10 \pi]$ of the equation $|2 \sin x-1|+|2 \cos 2 x-1|=0$. Round the answer to three significant digits according to the rules of rounding and enter it in the provided field.
|
{"ground_truth": "27.7"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 395
|
numina_1.5_454
|
verifiable_math
|
2. Find the length of the broken line on the plane, the coordinates of the points $(x ; y)$ of which satisfy the condition: $\left\{\begin{array}{c}|2 y-| x |-x=2 \\ -2 \leq x \leq 1\end{array}\right.$. Round the answer to three significant digits according to the rules of rounding and enter it in the provided field.
|
{"ground_truth": "7.24"}
|
{"source": "olympiads", "problem_type": "Geometry"}
| 396
|
numina_1.5_455
|
verifiable_math
|
3. The sum of two natural numbers is 2013. If you erase the last two digits of one of them, add one to the resulting number, and then multiply the result by five, you get the other number. Find these numbers. Enter the largest of them in the provided field.
|
{"ground_truth": "1913"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 397
|
numina_1.5_456
|
verifiable_math
|
4. The sum of two natural numbers is 2014. If you strike out the last two digits of one of them, multiply the resulting number by three, you get a number that is six more than the other number. Find these numbers. Enter the smallest of them in the provided field.
|
{"ground_truth": "51"}
|
{"source": "olympiads", "problem_type": "Algebra"}
| 398
|
numina_1.5_457
|
verifiable_math
|
5. Find the fraction $\frac{p}{q}$ with the smallest possible natural denominator, for which $\frac{1}{2014}<\frac{p}{q}<\frac{1}{2013}$. Enter the denominator of this fraction in the provided field
|
{"ground_truth": "4027"}
|
{"source": "olympiads", "problem_type": "Number Theory"}
| 399
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.